- Capillary pressure in wound dressings -

An investigation on behalf of Protex Healthcare Ltd.

This article deals with the autogenous capillary effect of wound dressing materials and shows the conversion of the calculated suction tension into comparable pressure units. For this purpose, the technique known as the “Washburn method” is used with the IMETER method M7.
By M. Breitwieser, IMETER MessSysteme and D. Viaene, Protex Healthcare Ltd., 5/2021.

About wound dressings

Modern wound treatment products are characterized by their absorption capacity and the creation of a moist wound environment. One of the main tasks of these wound dressings is to remove wound fluid (exudate), blood, and secretions from an injury (ulcer, edema, pressure ulcer, diabetic foot, burns, etc.) in order to enable the fastest possible healing. The aim is to keep the wound moist, but not wet. The types of wound treatment available can be briefly classified as follows [1,2]:

• Hydrophilic foams absorb exudate on the inner surfaces of the foam (regular capillary action hardly occurs here).
• As a quasi-polymeric salt, superabsorbents absorb aqueous solutions and swell to form a hydrogel.
• NPWT pumps create negative pressure through manual or electrical components. For this purpose, the treated body surface must be atmospherically insulated or sealed airtight.
• Specifically developed wound dressings such as VACUTEX™ use the capillary effect.

With compresses, foams or products with superabsorbents, the exudate is transported away physically, depending on the material, and with Negative Pressure Wound Therapy (NPWT) [5] by mechanical, mostly electrical pumps. The absorption and transport of the liquid are the essential functions of these wound dressings. Wound healing is promoted by the removal of the exudate by preventing bacterial growth and biofilm formation and also by removing elements that interfere with wound healing such as MMPS (matrix metal proteases) from the injury. The NWPT method draws in tissue fluid through external negative pressure and sucks off excess secretion. The treatment site remains wetted by secretion and there is no exchange of air. In the field of NPWT, it has been emphasized that certain negative pressures can have beneficial effects on wound healing; the medical benefit compared to conventional wound therapy is sometimes considered controversial in the literature [6]. VACUTEX™     (Picture: © Protex Healthcare Ltd.)

The sample material

1. VACUTEX™ 2015 (Ready-made nonwoven, 10x10 cm. Material thickness 3.0 mm, REF: VAC010010, LOT: 159847, Protex Healthcare).

2. VACUTEX™ 2020 (not assembled, in the form of 30x22 cm sheets, material thickness 3.0 mm, Protex Healthcare).

Technically, VACUTEX™ is a textile fabric made of a modern nonwoven laminate based on synthetic / natural fibers. VACUTEX has a three-layer structure and contains a Poly/cotton fabric (Gabardine) in the middle layer. See link product & applicational information on VACUTEX.
Solution A is a physiological calcium and sodium chloride salt solution according to DIN EN 13726-1; Hexane: Sigma-Aldrich, Reagent Plus ≥99%; Water: distilled, air saturated, conductivity ≤ 1 µS/cm.

Determination of the capillary pressure by sorption measurements

With sorption measurements according to the Washburn method [3,4], the absorption of certain liquids by a sample material is examined directly. The analytical method therefore directly addresses the intended use of the wound dressing material.
[Principle] A porous material touches the surface of a liquid - whether liquid penetrates into the cavities of the material and whether it is absorbed depends on whether the solid substance is wetted by the measuring liquid.

Porous is to be understood in general. It means that a material has holes, crevices or voids in contact with the surface. The examined substances are treated here as porous material. Wetting means that a drop of liquid flows apart on a solid surface - e.g. a drop of water on a stone. The flatter a drop lies on a smooth surface, the better it wets, i.e. the smaller the contact angle. The contact angle is 0° when the liquid completely dissolves (spreads). If a drop is in the form of a hemisphere, the angle is around 90°. In the case of porous materials, the contact angle cannot be observed; Wetting is synonymous here with being absorbed, the quality of the wetting then has more to do with the relative speed of the absorption (infiltration). Why does this even happen and what does it have to do with capillary pressure? --- A stone falls down and not up - only that which releases energy happens voluntarily. A liquid that spreads on a solid does so because it releases energy; this energy can sometimes even be measured as heat of wetting with a thermometer. Because of surface tension, an amount of liquid minimizes its surface area. A small drop takes on the shape of a sphere when no other force acts. When the drop is deformed, it requires a force. A force that acts on a surface –– is called pressure. If we now look at a liquid surface, for example a coffee in a porcelain cup, it appears flat and flat due to gravity. At the edge of the cup, however, the edge of the hem rises a little out of the plane. The coffee is pulled up a little against gravity on the edge of the cup. So there is obviously pressure on the surface.  Because if there was no pressure, the coffee would be at right angles to the edge of the cup. The force to deform the surface of the liquid comes from the wetting (adhesion) and the deformed surface simply means that pressure is acting. If the numerical value of the surface tension is known, a certain pressure can be assigned to the curvature of the surface. Surface tension and curvature cause the wetting to create a pressure that allows the liquid to rise in a vertical capillary tube until the force on the wetting line corresponds to the hydrostatic pressure.

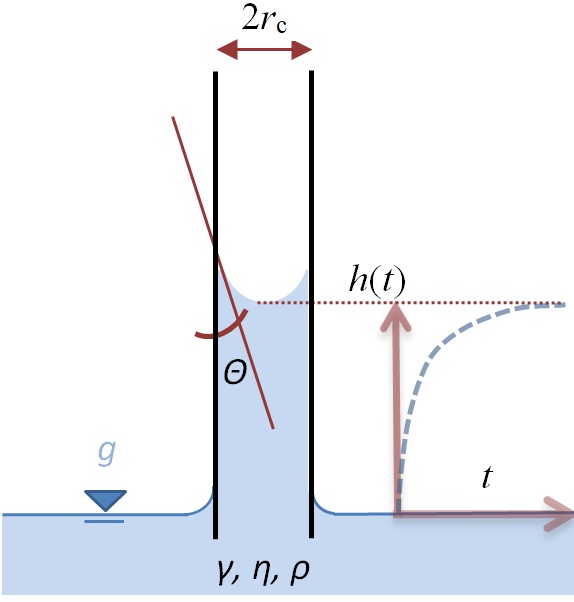The symbols in the Washburn equation

The better the solid can be wetted - i.e. the smaller the contact angle Θ - the greater the pressure of the liquid in the cavities. This pressure increases with the surface tension of the liquid (γ), the wetting quality (Θ) and the smallness of the pores (r̅_c). The viscosity (η) of the fluid together with the narrowness of the pores and the increasing length of the path through the solid structure slow down the infiltration process more and more. Finally, gravity inhibits and limits the rise of the liquid. The infiltration comes to a standstill as soon as the hydrostatic pressure of the liquid column corresponds to the capillary pressure.
[Calculation method] The porous absorption is formally physically manageable by the so-called Lucas-Washburn equation. It provides a description of the observation
according to the equation h = √ (t · r̅_c · γ · cosΘ / 2η) .
This means that the height of rise h after a time t is proportional to the root of the duration (√t), the effective capillary radius r̅_c and the surface tension γ of the liquid. 'cosΘ' is the cosine of the contact angle of the liquid on the solid. If this angle is equal to zero (Θ = 0 °), i.e. the wetting is total, cosΘ = 1 becomes maximum. With a liquid that completely wets the solid material, the effective capillary radius r̅_c can be calculated. The measurement can then be repeated with a liquid in question in order to determine the effective contact angle Θ by means of r̅_c (or a material constant K). Furthermore, the surface energy of the porous material can be calculated from at least two Θ values ​​with suitable liquids, to which the wetting and adsorption behavior can generally be attributed. The capillary pressure Δp is calculated using the determined capillary radius r̅_c and contact angle and with the surface tension of the liquid γ according to the Young-Laplace equation: Δp = 2 γ cos Θ / r̅_c  .Setup of a sorption measurement with IMETER M7 (Click for description).

The pressure is a calculated quantity, which is determined with the calculated contact angle and the also calculated effective capillary radius r̅_c. Here r̅_c is an effective value that would only be identical to the actual, geometric capillary radius if a measurement were applied to a bundle of ideal circular capillaries. In a textile fiber structure there are of course no such round, straight tubes, but all possible cavity shapes. The calculation of the pressure according to the given equation implies circular, straight capillaries.

[Measurement method] The plate-shaped or cubic sample piece is suspended in a temperature-controlled environment above the liquid surface on a weighing device (see picture on the right). After a tempering / conditioning phase in the atmosphere of the measuring cell, the liquid surface is moved upwards. The movement stops on surface contact and the liquid can rise up in the sample. The infiltration is then followed on the basis of the increase in weight. The M7 PUK method provides several characteristics of the sample material based on parameters that are legally related to one another from the properties of the liquid, the conditions of sample preparation, weight and infiltration measurements. The bulk density is specified with the sample geometry. The volume of liquid absorbed in relation to the sample volume allows differentiated information on porosity, and the absorption rate related to the contact area results in the sorptivity S.

Experimental execution

[Practical implementation] For the investigation, test pieces in the format 36 x 15.5 mm were cut out of the sample materials. The time course of the liquid infiltration after contact of the sample and the fluid was determined gravimetrically in an environment heated to 25.0 ° C. To determine the contact angle and therefore the effective capillary radius' r̅_c, measurements with hexane were carried out on the sample materials in order to determine the material constant (hence r̅_c) with cosΘ = 1. Details of the algorithm can be found here under modified Washburn equation. 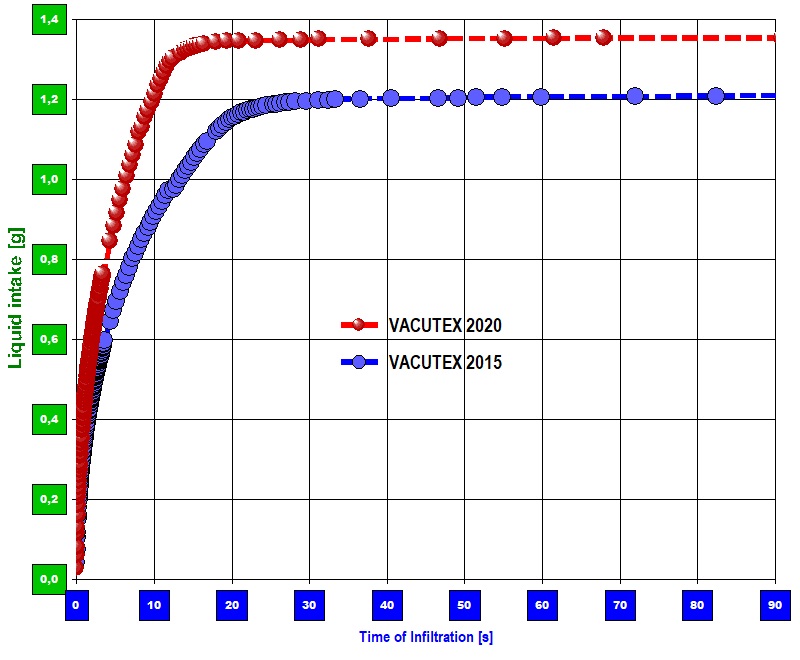Diagram 1: Speed of sorption on the temporal course of the sample weight. Combination of two measurements

From the derivation of the formula-based relationship, it should be noted for reality that r̅_c dubbed the effective capillary radius, does not represent a mean radius, but indicates the radius that straight tubes must have in order to exhibit the observed behavior. It should also be taken into account that the assumption of total wettability by hexane is assumed axiomatically, but cannot be verified. The surface tension of the fluid was determined before and after the sorption measurement directly in the same measuring cell (IMETER M1). In order to obtain more complete information about the porosity of the sample material, the absolute density of the products was also determined by hydrostatic weighing (IMETER M9, density at 25°C: ρ₂₀₁₅ = 1.388, ρ₂₀₂₀ = 1.390 g / cm³; porosity Φ₂₀₁₅ = 84.2% , Φ₂₀₂₀ = 83.4%). With regard to the measurements of the surface tension of solution A and water - before and after the infiltration - it was shown that both VACUTEX 2015 and VACUTEX 2020 evidently release trace amounts of surface-active substance to the aqueous liquid. The calculation of the capillary pressure was carried out with the resulting reduced surface tension. Without this reduction in surface tension, noticeably higher values ​​would result for the capillary pressure. Table 1 lists the measurement results from the sorption measurement. Some IMETER test reports are available in the Supplement.

Diagram 1 shows two typical "infiltration curves" of VACUTEX 2015 and VACUTEX 2020 in one chart. The curves represent the course of the sample weight over time. The contact between the liquid surface and the sample takes place at time "0" in the diagram. As the liquid (Solution A) in the sample is absorbed and rises, the sample piece becomes heavier and the 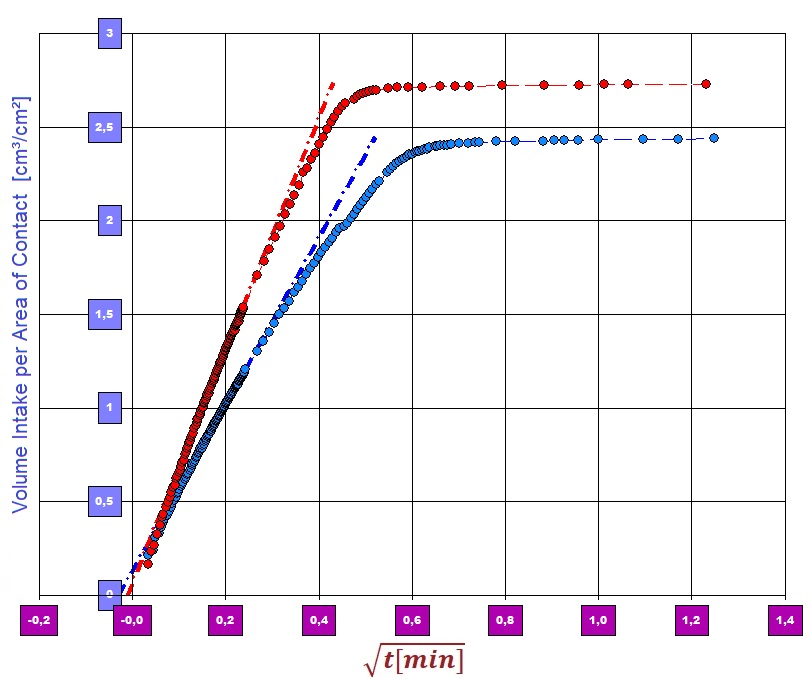Diagram 2: Sorptivitycurve increases accordingly. Both curves rise very steeply at first. After a few seconds, a separation of the courses can be determined. At second 10 or 20 the proportional increase breaks off and indicates that the fluid intake has ended. The kink in the graph indicates that the flow front has been reached at the geometric end of the sample. The liquid has risen completely in the sample - i.e. up to a height of 35 mm, the sample length. Diagram 2 shows the data and the evaluation of the performance on sorptivity. In addition to the speed of the sorption process, which is expressed in the steepness of the curve, the infiltration amount reached at the end of the curve in diagram 1 directly indicates the amount of liquid absorbed. One gram of VACUTEX 2020 absorbs approx. 3.3 cm³ of Solution A, VACUTEX 2015 with 3.2 cm³ noticeably less. The proportion of the volume remaining unfilled can be determined from the sample volume, porosity and quantity taken up. With VACUTEX 2020, around 5% of the free volume remains unfilled, with VACUTEX 2015, however, 16%.

[Critical check / plausibility test of the pressure calculation] The capillary pressure is calculated ideally based on the Young-Laplace equation. The capillary radii required for this are taken from the Washburn equation as "effective capillary radii". The calculated capillary pressure can thus be attacked as a purely theoretical construct. A criticism that could be cited, for example, is that circular capillaries are nowhere to be found in the fleece material. With the I-SIF sensor interface, the IMETER measuring system has a precision sensor for measuring the air pressure. However, this can be destroyed by higher pressures. For our critical review, we believed our calculations - that is, 5-10 kPa overpressure would not destroy the sensor. For example, a VACUTEX 2015 test piece was encased in a viscous epoxy resin, one side being left free and a pipe for connecting the pressure sensor inserted on the opposite side. After the synthetic resin had hardened, the pressure sensor was tightly connected to the connection pipe using a silicone hose. 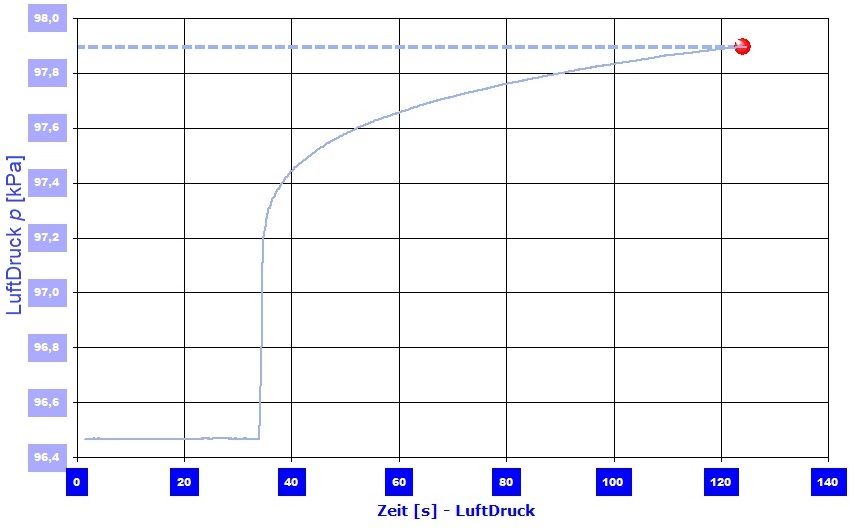Diagram 3: Pressure measurement - steep pressure increase on contact with the liquid.The I-SIF function of the IMETER software takes over the measurement and recording of the pressure 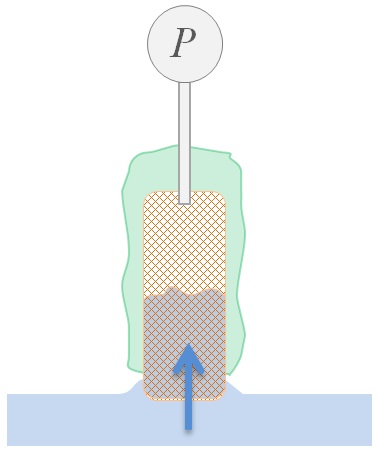for simple measurements. This was started and the area that had remained free from the casing was brought into contact with a surface of water. The water is absorbed by capillary action and displaces the air in the fleece. However, the displaced air cannot escape and thus increases the pressure - the air pressure - in the sealed space. In this way, the capillary suction can be measured as excess air pressure, as shown in Diagram 3. For VACUTEX 2015, an overpressure of up to 2 kPa was measured in this way. This corresponds to almost half the value from the theoretical calculation (4.8 kPa). Various reasons can be given why the pressure was measured in this way smaller than it should be (the maximum pressure occurs at the beginning of the infiltration and the dead volume in the structure is relatively large and the hydrostatic pressure of the ascending fluid is the measured pressure to add ...). Overall, it can be said that the conventional pressure measurement supports the assumption of the fundamental correctness of the capillary pressure determination carried out in this article.

By the way, that negative pressure is created by capillary action, it becomes immediately clear to everyone (child) when the tongue or the damp lip touches blackboard chalk, a pottery shard or some other wettable, fine-pored material. The tongue sticks - and that is suction through the effect of the noticeably negative capillary pressure.

Result of the capillary pressure determination

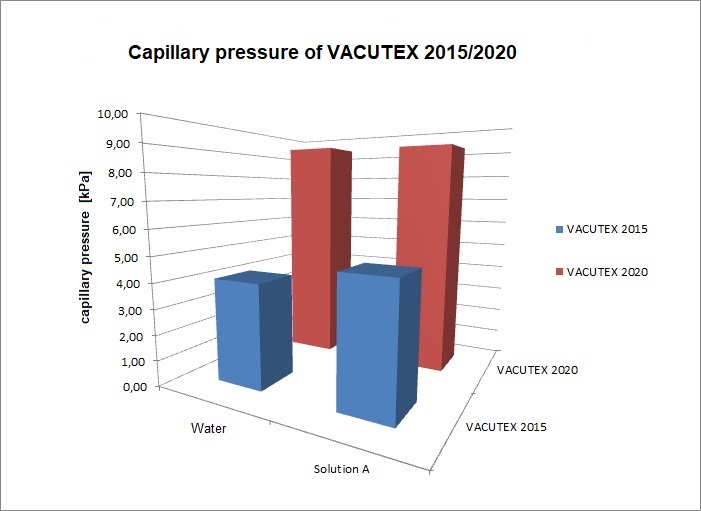Diagram 4: "Performance"

The pressure at which a dressing material absorbs liquid by capillary action can be determined by sorption measurements. To dimension the same, i.e. to quantify the capillary suction effect, the application of the Washburn equation was used in order to be able to make product comparisons on the physically measurable material properties. Using the effective capillary radii, it enables the pressure to be determined according to the Young-Laplace equation. The results of the investigation revealed the following for the two VACUTEX products: Compared to a physiological saline solution (Solution A), VACUTEX 2020 achieves a pressure 9.1 kPa (68 mmHg). This pressure range corresponds to around 5 to 10% of the atmospheric air pressure and is therefore also in the range of the NPWT (25 to 125 mmHg). VACUTEX 2020 achieves against a physiological saline solution (Solution A) almost twice the capillary pressure Δp compared to the previous product VACUTEX 2015 (see diagram 4). The capillary pressure of the physiological salt solution is noticeably higher than that of water. This means that a higher salt load does not affect the pumping speed. But on the contrary. If the effective capillary radii r̅_c of the two nonwovens are approximately comparable, the cause of the differences in performance is due to the respective contact angle. The smaller the contact angle Θ, the greater the capillary pressure or the suction intensity. At 65.1°, VACUTEX 2020 achieves a more favorable value compared to the physiological saline solution (Solution A). At 74.6°, VACUTEX 2015 is noticeably less wettable. Compared to pure water, the relative differences are even more pronounced. Here the contact angle of VACUTEX 2020 is even improved by 17.8°.

Conclusions and Outlook

VACUTEX 2015 and 2020 are characterized by a high capillary effect, with the technically optimized VACUTEX 2020 showing significantly improved effectiveness in terms of suction power and absorption capacity. It turns out that not only complex technologies such as NPWT can generate higher pressures, but passive systems are also able to do so. VACUTEX offers a good alternative for NPWT, also in less privileged regions of the world, in countries where healthcare budgets are under pressure or where NPWT is not available to everyone. The observed heights of rise of several centimeters go hand in hand with the fact that in the extensive VACUTEX application (which may be applied in multiple layers to injuries) the suction tension in the exudate-soaked wound dressing is dynamically reproduced through evaporation of the wound water. Since injuries can secrete a lot of exudate overall, but the amount of fluid produced per unit of time is often relatively small, a cumulative higher absorption capacity can be achieved. As a likely beneficial additional effect, the wound is cooled by the evaporation at the same time (inflammation - bacterial growth, pain relief). To what extent the capillary action and the associated transport processes may also lead to a healing-promoting stimulation of the wound tissue must be clarified by clinical investigations.
"VACUTEX 2025" -? - A particular challenge could be anticipated by means of the automated sorption measurement instrumented with the IMETER measuring system, namely the selective adsorption of wound healing-impairing species that could be bound to VACUTEX fibers from the moist wound environment. The work required for this on the identification and determination of the surface energy of the relevant proteins, cell components, enzymes etc. and the respective liquid should, however, be a non-trivial task [5,6].

Supplement

Examples of fully documented test reports in PDF format that the IMETER measuring system automatically generates for measurements:
- Sorption measurement VACUTEX2015 (ID17757)
- Sorption measurement VACUTEX2020 (ID17761)
- Density measurement on VACUTEX2020
- Measurement of the surface tension of the water after sorption measurement

Literature

Links

This article: https://www.imeter.de/VACUTEX2020eng,  Dieser Beitrag auf Deutsch: https://www.imeter.de/VACUTEX2020de
Companies: www.protexhealthcare.com, www.imeter.de