Oberflächenspannung ist die Eigenschaft einer flüssigen Phase, Grenzflächenspannung charakterisiert Verhältnisse zwischen zwei fluiden Phasen. Bei Drei-Phasen-Systemen, die mit dem Zusammentreffen fluider, gasförmiger und fester Phasen bzw. zweier fluider und einer festen Phase auftreten, werden die energetischen Verhältnisse durch Kontaktwinkel der fluiden Phase charakterisiert.
|
<Oberflächenspannung entspricht quasi dem Biegeradius> |
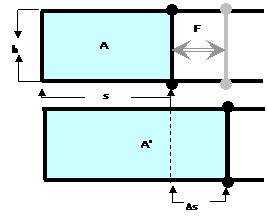
Veranschaulichung der Oberflächenspannung: In einem Drahtrahmen (Maxwell'scher Rahmen) ist ein Flüssigkeitsfilm aufgespannt (Abb. links). Indem der Bügel im Rahmen verschiebbar ist, kann der Film auseinandergezogen werden. Um den Bügel nun um die Strecke Δs gegen die Kraft F zu bewegen, muss Arbeit geleistet werden (Arbeit=Kraft x Weg, also W = F·Δs). Durch die geleistete Arbeit wird neue Oberfläche geschaffen. Die neue Oberfläche (ΔA=A-A') ist ΔA = 2·Δs·h; "2·Δs", weil neue Oberfläche auf der Vorder- und Rückseiten des Rahmens gebildet wird. Die Oberflächenarbeit ist also: Wo= F·Δs = F·ΔA /(2·h) Nach Division durch ΔA ergibt sich: Wo / ΔA = F / (2·h) = γ Der Quotient "aufgewendete Arbeit pro erzeugte Oberfläche" ist eine Konstante: γ, die Oberflächenspannung der Flüssigkeit. Die Einheit ergibt sich dennach mit W/A => J/m2 =N·m/m2 = N/m bzw. mN/m und kann also auch Oberflächenenergie genannt werden. Die Oberflächenenergie ist reversibel - sie wird beim Zurückschieben des Bügels im gleichen Ausmaß, proportional zu ΔA und γ, wieder frei. Ohne Austausch von Wärme mit der Umgebung wird der Film durch Oberflächenvergrößerung abgekühlt bzw. umgekehrt erwärmt – wie bei einem zweidimensionalen Gas. Die Grenzflächenspannung bzw. -energie zwischen zwei Fluiden ist die in jeder Hinsicht analoge Größe zwischen den beiden Phasen. Abb. links, die Quantität der Oberflächenspannung: |
Ein beliebtes Missverständniss beim Thema "Oberflächenspannung": "Spülmittel verringert die Oberflächenspannung von Wasser und deswegen schäumt Spülwasser". Dem ist nicht so, denn die Oberflächenspannung des Wassers bleibt unverändert! Das ist keine Spitzfindigkeit über Spülwasser, welches ja kein Wasser mehr ist, sondern die Oberflächenspannung des Wassers kann bloß nicht mehr gemessen werden, weil das Wasser darin keine freie Oberfläche mehr hat. Die Oberfläche wird durch die Spülmittel-Tenside gebildet (oberflächenaktive Substanzen). Schäumen und die Möglichkeit Seifenblasen zu erzeugen hat kaum mit der Oberflächenspannung zu tun. Benzin oder Cognac schäumen ja auch nicht, obwohl die Oberflächenspannung ziemlich gering ist. Der Punkt ist 'Strukturbildung': Tenside bilden innerhalb des Wassers kleine Tröpfchen (Mizellen) und an Oberflächen (mehrlagige) Filme.
B. Bestimmungsmethoden, Verfahren (Fluide)
Der klassischen Literatur[z.B.14] ist bereits zu entnehmen, dass dem Phänomen Oberflächenspannung und der zugehörigen Messtechnik einiges Interesse beigemessen wurde. Man findet Namen wie Da Vinci, Newton, Gay-Lussac, Gibbs, Gauß, Röntgen, Kelvin, Rayleigh, Laplace, Pascal, Young und Einstein. Zur Bestimmung der Oberflächenspannung sind aber nicht deshalb so viele verschiedene Methoden entwickelt worden. Es gibt schlicht viele Zusammenhänge und Schwierigkeiten. Neben den heute bekannten Messverfahren, sollen in der nachfolgenden Auflistung auch historische erwähnt werden wie auch solche, die nicht ausschließlich für die Messung der Oberflächenspannung vorgesehen sind. Die Grenz- und Oberflächenspannung wird aus direkt messbaren Kräften oder aus Effekten der Kraftwirkung ermittelt:
- Benetzungskraft bzw. Meniskusgewicht (DeNoüy-Ring, Wilhelmy-Platte, Lenard-Bügel)
- direkte Kapillarwirkung (Steighöhenmethode)
- Druck in Hohlräumen (Blasendruck)
- Tropfengewicht (Tropfenvolumen, Stalagmometer)
- Ober-/Grenzflächengestalt (pendant drop. Oberflächenwellen, dynamisch Lichtstreuung)
Man unterscheidet dynamische und statische Verfahren. "Dynamisch" heißt, dass bei der Messung permanent neue Oberfläche geschaffen wird. "Statisch" bedeutet, dass zur Messwertablesung eine Oberflächen-Neubildung nicht erfolgt und ein Kräftegleichgewicht herrscht. Für Referenz- bzw. Präzisionsmessungen und für Daten zu Simulationsrechungen werden statische Messungen bevorzugt. Insbesondere die Steighöhenmethode in Kapillaren gilt als Referenzmethode (Methode 3.).
1. Ring-Methode (Lecomte De Noûy), Bügelmethode (Lenard), Tensiometer
γ = Fmax.· f1· f2 / (4·π·R)
Die Ober- bzw. Grenzflächenspannung (γ) ergibt sich aus der Maximalkraft (Fmax.), dem Ringumfang (mittlerer Radius R) und mit zwei Korrekturfaktoren ( f1, f2 ). Der Korrekturfaktor f1 korrigiert eine systematische Abweichung. Um f1 zu berechnen, gibt es verschiedene Verfahren, die nach den Autoren: Harkins und Jordan[5], Fox und Chrisman [8], Zuidema und Waters[7] und Hue und Mason benannt wurden.[69,70] Dabei wird die Korrektur im Wesentlichen aus der Ringgeometrie (Radius und Ringdrahtstärke) und der Dichtedifferenz der Phasen berechnet und/oder Tabellenwerken entnommen bzw. mit dem Term Fmax./4·π·R und Konstanten ermittelt. Der zweite Faktor f2 wird durch Kalibrierung mit Referenzflüssigkeiten bestimmt und ist eine individuelle Korrekturzahl, wie sie bei praktisch allen physikalischen Mess-Rechenmethoden anzutreffen ist. Diese berücksichtigt hier als proportionale Abweichungen die Diskrepanz von idealer und realer Ringgeometrie durch Geometrie-Messfehler sowie geringe Unrundheiten und Unebenheiten (Dieser Faktor darf von 1 nicht mehr als um 0.1% abweichen, sonst stimmt 'was grundsätzliches nicht). Zu Ergebnisangaben gehört unbedingt auch die Nennung des Berechungsverfahrens, da gleiche Ergebniswerte sich dadurch unterscheiden können. So z.B. Wasser, mit einem Standardring DIN gemessen, liefert als Ergebnis nach den Tabellen von Harkins und Jordan 73,00 und nach Zuidema 72,75 mN/m.
Andere dynamische Kraftmethoden: Beim Lenard Bügel befindet sich zwischen zwei parallelen Stangen in einem rechtwinkligen Drahtrahmen ein dünner, waagerecht verlaufender Draht. Das Verfahren ist analog zur Ringmethode. De Gennes [84, S.62] beschreibt eine allgemeine Handhabung der Maximalkraftmethode mit Bewegung, also dynamisch für verschiedene Gegenstände, so auch eine alternative 'Maximalkraft'-Handhabung der nachfolgend skzzierten Wilhelmy-Methode.
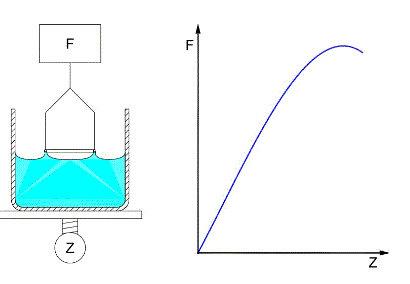
Diagramm (Anklicken, um eine Animation zu zeigen ): typisches Aussehen einer Messkurve mit der Ringmethode : Wird der Ring aus der Flüssigkeit gehoben, wächst die Kraft anfangs relativ gleichmäßig an, fällt in einer gewissen Entfernung dann mehr und mehr ab und beschreibt etwa einen Parabelbogen. Die Parabelspitze markiert den gesuchten Maximalwert der Kraft. [Interessant am Kraftverlauf ist, dass eine Bewegung nach dem Parabelmaximum auf dieses zurück, die Kraft jetzt mit der Annäherung ansteigen lässt, also eine Abstoßung auftritt.]
Doch Vorsicht mit dem Begriff 'Abrissmethode'! Die Bezeichnung rührt noch von den Zeiten der Torsionsdraht- und 'Chainomatic Waagen' her, bei welchen es bei geringfügigem überschreiten der Maximalkraft durch die anliegende elastische Höchstlast kein Halten mehr gibt und die Lamelle in der Maximalkraft abbricht. Gleichwohl wird der wahre Wert angenähert erreicht bzw. leicht überschritten. W. D. Harkins hat diese Methode angewendet. Demgegenüber – auf heutigen, wegfreien Kraftmessern/Waagen – sagt die Abreisskraft nichts genaues über die Oberflächenspannung aus.
DIN 53914, Bestimmung der Oberflächenspannung - Prüfung von Tensiden.
DIN 53993, Bestimmung der Grenzflächenspannung - Prüfung von Tensiden - Bügel oder Ringmethode.
ISO 6889 Surface active agents - Determination of interfacial tension by drawing up liquid films.
ASTM D0971-99AR04 Test Method for Interfacial Tension of Oil Against Water by the Ring Method
ASTM D1331-89R01 Test Methods for Surface and Interfacial Tension of Solutions of Surface-Active Agents
ASTM D1590-60 Test Methods for Surface Tension of Water and Waste Water
Eine Vereinfachung der Ring-Methode bietet die sog. "Du Noüy-Padday method", die mit sehr kleinen Ringen arbeitet und minimaler Probenmenge auskommt (Einzelheiten, Literaturangaben vgl. en-Wiki). Die Arbeitsgleichung lautet dabei schlicht "γ = Fmax.· f2 / (4·π·R)". Hier wird also keine Dichteangabe und kein Korrekturfaktor außer f2 benötigt. Messungen gemäß diesem Verfahren sind mit der IMETER-M1 kompatibel ausführbar. Denn M1 erlaubt beliebige Ringgrößen und separat die Auswahl der verschiedenen Berechnungsalgorithmen, darunter "Fmax/2L", der also nach dem Padday-Verfahren rechnet (neben den oben genannten Korrekturalgorithmen).
DIN 53914, Bestimmung der Oberflächenspannung - Prüfung von Tensiden
Die Methode wird zur Messung der Oberflächenspannung, aber auch für Kontaktwinkelmessungen eingesetzt (Wilhelmy-Platte Typ II, vgl. Punkt 11). Es wird eine senkrechte Platte mit der Oberfläche einer Flüssigkeit in Kontakt gebracht. An der Kontaktstelle bildet sich ein Meniskus. Durch den Meniskus wirkt zwischen Platte und Flüssigkeit eine Kraft, die von der Benetzung herrührt und zusammen mit dem Umfang der Platte einfach die Oberflächenspannung zu berechnen ermöglicht - sofern die Platte total benetzbar ist. Die Oberflächenspannung (γ ) ergibt sich aus der Kraft (F) und dem Plattenumfang (p).
γ = F/p
Anstelle einer Platte, die i.d.R. aus Platin gefertigt und aufgeraut ist, können je nach Zweck auch andere Materialien Verwendung finden. Dünne Glas- und Glimmerplättchen, sogar Filterpapier [67, S.114] und bedingt auch Körper mit anderer Geometrien können eingesetzt werden. Wenn trotz einer Überprüfung der Funktion mittels Standardflüssigkeiten Zweifel an Resultaten auftreten – es gibt lt. Literatur Probleme durch kationische Tenside, die zu Benetzungsstörungen führen – kann eine Sicherstellung der korrekten Oberflächenspannungsbestimmung dadurch erfolgen, dass wie unter 11.b zur Messung die Platte ein- und ausgetaucht wird. Die reslultierende Hysteresekurve, Kraft gegen Eintauchtiefe bei der Ein- und Austauchbewegung, muss nahezu deckungsgleich ausfallen. Ein größerer Unterschied wäre ein sicheres Indiz für die Untauglichkeit der verwendeten Kombination von Platte und Probe.
Die durchaus einfach anwendbaare Wilhelmy-Methode gibt es als 'IMETER-App'. Sie nutzt unser Patent zur statischen Messung, ist kostenlos, recht komfortabel und schlicht anwendbar - mit assistiertem Messablauf und automatischer Auswertung - (Wilhelmy-Methode - eine 'IMETER App').
3. Steighöhe in Kapillaren (capillary rise method)
γ = h·r·g·ρ/2: Die Oberflächenspannung (γ ) ergibt sich aus der Steighöhe (h), der Dichte (ρ) und Fallbeschleunigung sowie dem Röhrenradius (r).
Praktisch werden Messungen mit mehr als einer Kapillare ausgeführt. Setzt man zwei Kapillaren – natürlich mit bekannten doch unterschiedlichen Durchmessern – ein, kann die leichter ablesbare Steighöhendifferenz zur Berechung verwendet werden. Ein Viskositätsproblem bleibt natürlich bestehen. (Zur Ausführung und exakten Berechnung [15, S.64], [83, S.221]).
Historisch kommt der Steighöhe in Kapillaren eine herausgehobene Bedeutung zu. An ihr entzündete sich die Theoriebildung.[84 , S.49]: Leonardo Da Vinci glaubte, Quellwasser in den Bergen würde gefördert durch das Netz feiner Kapillaren im Untergrund*. J. Rohault (1620-75) interpretierte den Kapillaranstieg als bedingt durch den Unterdruck, der sich in den engen Räumen bilde, da die Luftzirkulation fehle**. Giovanni Borelli (1608-79) stellte fest, dass die Steighöhe sich umgekehrt zum Kapillardurchmesser verhält. Zum immer noch gültigen Ergebnis führte die systematische Untersuchung von Francis Hauksbee (1660-1713), die letztlich Newton in seiner "Opticks" beschrieb (Hauksbee, seinen Assistenten, jedoch zu erwähnen vergaß). Zur Ableitung des Gesetzes der kapillaren Steighöhe vgl. Jurin's Gesetz.
*Es gab zwischenzeitlich noch andere Perpetuum-Mobile Ideen auf Basis der Kapillareffekte, z.B. von Sir William Congreve - mit einer Kette aus Schwämmen (1827, Engl. Pat.No 5461).[51 S.129]
** Ein interessanter Gedanke hinsichtlich der kinetischen Gastheorie.
4. Tropfenmasse: Tropfenvolumen-Tensiometer, Stalagmometer
Dabei wird Flüssigkeit aus einer Kanüle gedrückt. Diese fließt durch ein speziell geformtes Kapillarrohr an dessen Ende die Tropfen in möglichst niedriger Rate abfallen. Die gravimetrisch oder volumetrisch erfasste Tropfengröße (unter Kraftwirkung der Erdanziehung) erlaubt die Berechnung der Oberflächenspannung. Die Methode ist entsprechend nur dann, wenn sehr langsam ausgeführt, eine statisches Messverfahren.
W = 2π·r·γ·f ("Das Gewicht W eines abfallenden Tropfens ist proportional zum Röhrenradius r ..." = Tate's Gesetz (1864).)
bzw.:
γ = f · V
ρ /n : Die Oberflächenspannung (γ) ergibt sich aus dem ausgeflossenen Volumen (V), wobei eine Anzahl von Tropfen (n) gebildet wurde. Die Dichte (ρ) wird immer gebraucht – und ein Faktor f, der durch Kalibrierung mittels Referenzflüssigkeiten ermittelt wird. Eine Gerätebeschreibung und genaue Anleitung gibt Harkins [15, S.71ff]. Die Methode erlaubt vermutlich ganz analog auch die Bestimmung der Grenzflächenspannung zwischen Fluiden; in der Formel ist für ρ entsprechend ∆ρ . einzusetzen.
ASTM D2285-99 Test Method for Interfacial Tension of Electrical Insulating Oils of Petroleum Origin Against Water by the Drop-Weight Method
5. Druck in Hohlräumen: Blasendruck Tensiometer
Besser als die letztgenannte Methode ist diese zur Erfassung geschwindigkeitsabhängiger Effekte geeignet - wenngleich sie letztendlich, wie eigentlich alle Messmethoden, statisch definiert ist. - Durch eine Kanüle wird ein Gas in die Flüssigkeit gedrückt; die Bläschen wachsen und lösen sich ab wobei die Druckschwankungen gemessen werden. Der Gasdruck und die Bildungsgeschwindigkeit der Blasen hängen über die Oberflächenspannung zusammen. Erhalten wird die (quasi-) Oberflächenspannung auch als Funktion der Oberflächenbildungsgeschwindigkeit. - Bereits vor einem Jahrhundert wurde mit dieser Methode bei sehr hoher Temperatur an geschmolzenen Mineralien die Oberflächenspannung gemessen [40, S.129]. F. M. Jaeger: "Wenn die Methode durch äußerst langsame Druckänderung der eingeblasenen Luft so viel wie nur möglich zu einer statischen geworden ist, d.h. wenn man dabei so langsam verfährt, dass man den Endzustand durch eine ganze Reihe von wirklichen Gleichgewichtszuständen der Blase erreicht, so besteht zwischen der Oberflächenspannung und dem gemessenem Maximaldruck eine einfache Beziehung...".
γ = (∆p-ρ·g·h)·r/2 : Die Oberflächenspannung (γ) ergibt sich aus dem Überdruck (∆p), dem Kapillar- = Blasenradius (r), sowie Dichte (ρ), Fallbeschleunigung (g) und Eintauchtiefe der Röhre (h).
Der maximale Druck tritt bei Gleichheit von Kapillar- und Blasenradius auf. Auf dem fundamentalen Zusammenhang von Drucken und Blasen- bzw. Oberflächenformen basieren auch einige andere Methoden. Sie führen zur Young-Laplace-Gleichung: ∆p = γ·(1/r1+1/r2), wobei der Druckunterschied (∆p) über einer gekrümmten Oberfläche aus der Oberflächenspannung und den Hauptkrümmungsradien (r1, r2) beruht (r1 und r2 sind zueinander orthogonale, vorzeichenbehaftete Krümmkreise zur Normale im Flächenpunkt, vgl. Skizze für Kapillaren, Abb.A).
ASTM D3825-90R00 Test Method for Dynamic Surface Tension by the Fast-Bubble Technique
6. Methode des hängenden Tropfens (Pendant Drop)
Die Gestalt eines am Ende einer Kapillare hängenden Tropfens unter dem Einfluss der Erdbeschleunigung ist durch die Oberflächenspannung bestimmt. Die Messwerte zweier Durchmesser des hängenden Tropfens, dem maximalen und dem Durchmesser des Tropfens in der Höhe der Mitte der Tropfenunterseite, sowie die Dichte der Flüssigkeit müssen bekannt sein, oder gemessen werden. Um zu entscheiden, ob die Tropfenform einem Gleichgewichtszustand entspricht, existieren Kriterien. - Zur Bestimmung der Grenzflächenspannung kann der Tropfen unter Zuhilfenahme einer Küvette in einer zweiten Flüssigkeit hängen.
γ = ρ· g· l / (1/r1 +1/r2) : Die Ober- bzw. Grenzflächenspannung (γ) ergibt sich aus der vertikalen Tropfenlänge bzw. Höhe (l) mit Dichte (ρ), Fallbeschleunigung (g) und den Krümmungsradien des Tropfens (r1, r2) an seiner größten Breite.
7. Sessile Bubble
Eine Blase wird unter einer planen, benetzten Platte angebracht.
γ = ∆ρ·g·r²/(b·f1²) = ∆ρ·g·h²/(b·f2²) : Die Ausmaße des äquatorialen Radius (r) und der Abstand des Blasenäquators zur Blasenunterseite (h) dienen zur Berechnung der Oberflächenspannung bzw. zur Berechnung der Grenzflächenspannung zwischen zwei sich nicht mischenden Flüssigkeiten (∆ρ Dichtedifferenz). Die Geometriefaktoren b, f1 und f2 werden aus r und h berechnet.
8. Methode des liegenden Tropfens (sessile drop I)
Die Bestimmung der Oberflächenspannung kann auf Basis der optischen Ausmessung der am Rand gekrümmten, kapillaren Zylinderfläche eines liegenden Tropfens beruhen, der sich gemäß Dichte und Schwerkraft entsprechend deformiert.
9. Oberflächenwellen
Für Kapillarwellen bzw. Flüssigkeitswellen, die z.B. durch eine eintauchende Stimmgabel auf einer Flüssigkeitsoberfläche erzeugt werden, gilt (nach Kelvin):
γ = 1/(2π·g) · n²·λ³·r - λ²·ρ/(4·n²) *)
Die Oberflächenspannung (γ) ergibt sich hier als (optisch bestimmte) Wellenlänge (λ) auf der Flüssigkeitsoberfläche und zwar aus der Schwingungszahl (n, Frequenz der Stimmgabel) bei gegebener Flüssigkeitsdichte (ρ) und Erdbeschleunigung (g) ([Lit. 58] Mit Behandlung der von Planck aufgeworfenen Frage, nach dem Viskositätseinfluss auf die Messung der Oberflächenspannung).
*)Hinweis: die Einheit der Oberflächenspannung ist um 1900 und in der im Original wiedergegebenen Gleichung noch in der Dimension Gewicht pro Länge (g/cm).
C. Festkörper, Kontaktwinkel, Grenzflächenspannung
10. Kontaktwinkelmessung an liegenden Tropfen (sessile drop II)
Goniometer: Bei der weit verbreiteten Methode zum Studium der Benetzungseigenschaften wird ein Tropfen einer bekannten Flüssigkeit auf der zu untersuchenden Festkörperoberfläche platziert oder bisweilen auch ein Tropfen einer unbekannten Flüssigkeit auf eine definierte Festkörperoberfläche aufgebracht. Mittels einer optischen Vorrichtung wird über die Tropfenoberfläche hinweg der Winkel angepeilt, mit dem der Rand des Tropfens den Untergrund berührt (Skizze und Erklärungen vgl. Young-Gleichung/Benetzung).
DIN EN 828, Klebstoffe - Benetzbarkeit - Bestimmung durch Messung des Kontaktwinkels und der kritischen Oberflächenspnnung fester Oberflächen.
ASTM D 724-94 Standard Test Method for Surface Wettability of Paper (Angle-of-Contact Method)
Vorrück- und Rückzugs-Kontaktwinkel (advancing ϴadv, receding contact angle ϴrec) können durch Zudosierung oder Absaugung am liegenden Tropfen über eine Kanüle realisiert werden und es finden Neigungstische zu entsprechenden Zwecken Verwendung. Wenn die geprüfte Oberfläche nicht ideal und repräsentativ ist, ist die dann notwendige Bestimmung von Mittelwerten ein aufwändigeres Unterfangen. Weiterhin kann die Subjektivität der Kontaktwinkelablesung problematisch sein. -- Mit der Kontaktwinkelmethode sind noch andere Techniken verwandt, z. B. die Tropfenprofilanalyse, die neben dem Randwinkel noch weitere Informationen liefert.
'Höhe von Fluidschichten' (Puddles on a surface): Bei sehr großen Tropfen im Ausmaß des x-Fachen der kapillaren Länge √(γ/(ρ·g), sozusagen bei Pfützen auf Oberflächen, wird die Höhe h der Flüssigkeitsschicht durch den Kontaktwinkel ϴ und die Oberflächenspannung γ der Flüssigkeit nebst Dichtedifferenz ρ und Schwerkraft g bestimmt: h = √(2γ(1- cos(ϴ))/(ρ·g)) [Lit. 84, S.36]
(Wir werden diese Methode im Framework adaptieren, sobald dafür Gelegenheit ist. Spannend könnte sein, dass die Höhendifferenz h zwischen Untergrund und Flüssigkeitsoberfläche mittels eines elastischen Elements ziemlich genau bestimmbar ist und mit dem Tastkopf [evtl. einem Padday-Ring] parallel γ verifiziert werden kann.)
11. Plattenmethode, Wilhelmy-Platte (Typ II) / Wilhemly Slide und Steighöhen-Methode
11.a: "Wilhelmy-Typ II": Der Aufbau ist vergleichbar in Methode 2 beschrieben, der Messung der Oberflächenspannung mit einer Platte, nur dass hier nicht die vollständige Benetzbarkeit der Platte durch die Flüssigkeit angenommen wird. Die Platte ist aus dem zu untersuchenden Probenmaterial oder damit beschichtet und die Oberflächenspannung der Flüssigkeit muss bekannt sein. Der Kontaktwinkel wird berechnet nach: cos(ϴ) = F/(P·γ).
Die Kraftmessung (F) wird elektronisch realisiert. F ist die Kraft, die aus der Benetzung der Platte mit dem horizontalen Umfang P herrührt (Meniskusgewicht). Werden an einem Plattenmaterial mit verschiedenen Flüssigkeiten entsprechende ϴ-Werte bestimmt, kann daraus die Oberflächenenergie des Plattenmaterials ermittelt werden. Die in der Literatur erwähnten Ausführungen beschreiben die Messung als dynamisch. Die Platte wird mit konstanter (langsamer) Geschwindigkeit in die Flüssigkeit bewegt und herausgezogen. Vorrück- und Rückzugswinkel (ϴadv., ϴrec.) werden aus Extrapolationswerten der Kraft auf Eintauchtiefe Null bestimmt. Wir haben die Methode für das IMETER-Framework adaptiert und durch statische Messungen erweitert. Dabei wird die Oberfläche des Körpers, der keine Platte sein muss, abgetastet und jeder Tastpunkt liefert einen einzelnen ϴadv.- bzw. ϴrec.-Wert. Für übliche Prüfkörper erhält man so anhand von Mittelwert und Standardabweichung ein realistisches Bild. Finden Sie bitte auf unserer Seite "Contact Angle IMETER Methode N°4" eine genauere Auseinandersetzung mit dieser neu und universell gestalteten Technik.
11.b "Steighöhenmethode": Diese Methode zur Bestimmung des Kontaktwinkels beruht auf der Messung der Steighöhe des Flüssigkeitsmeniskus an einer senkrechten Oberfläche, z. B. einer Platte – nicht zu verwechseln mit der Steighöhenmethode in Kapillaren oder porösen Stoffen (Methoden 3. und 12.)! Die Steighöhe an der senkrechten Wand wird hier optisch gemessen (Kathetometer); sie liefert bei bekannter Oberflächenspannung der Flüssigkeit den Kontaktwinkel.
sin(ϴ) = 1 - ρ·g·h²/2γ : Der Kontaktwinkel (ϴ) ergibt sich aus der Steighöhe (h) mit Dichte (ρ) und Oberflächenspannung (γ) der Flüssigkeit.
Diese Steighöhenmethode wird auch als 'static Wilhelmy plate method' bezeichnet.[Lit. 83, S.318]
12. Sorptionsmessung, Washburn-Methode, Steighöhen-Methode
Die Eindring-, Aufsaug- d.h. Sorptionsgeschwindigkeit einer Flüssigkeit in ein poröses Material kann zur Bestimmung des Kontaktwinkels verwendet werden. Pulver, Filz, Flies, Fasergewebe, Papier, Sinterwerkstoffe bzw. poröses Material im Allgemeinen werden mit einer Flüssigkeitsoberfläche in Kontakt gebracht. Über eine definierte Kontaktfläche von porösem Körper und Flüssigkeit wird die Flüssigkeit durch die Kapillarwirkung der Poren aufgesogen. Damit der Sorptionsvorgang spontan und auch entgegen der Schwerkraft (aufwärts) abläuft, muss eine Benetzbarkeit der Feststoffoberfläche gegeben sein. Pulver werden für solche Messungen z.B. in einer per Fritte oder Sieb unten durchlässig geschlossenen Röhre untergebracht. Pulverhalter respektive Probenkörper sind mit einer Wägevorrichtung verbunden. Der zeitliche Verlauf der Gewichtszunahme wird aufgezeichnet.
cosϴ = m²·η/(t·K·γ·ρ²)
Die Variablen der sog. modifizierten Washburngleichung: Dichte (ρ), Viskosität (η) und Oberflächenspannung (γ) der Flüssigkeit werden als Eingangsgrößen benötigt. Dazu kommt die aufgesogene Flüssigkeitsmenge (m) während der Zeit (t), die gemessen wird. Porenart, Porendichte, Porosität, Oberfläche, Fallbeschleunigung und Gerätekonstanten werden in einem Faktor K vereinigt. Diese kummulative Materialkonstante K wird mit gleichen Probenmaterial/Zubehör und einer total benetzenden Flüssigkeit (cos ϴ = 1) in einer Kalibrierung ermittelt. Damit können in einer Messreihe Kontaktwinkel ϴ bestimmt werden bzw. die Oberflächenenergie aus mehreren Kontaktwinkelmessungen.
Eine ausführliche Beschreibung der Einzelheiten wird auf zwei Seiten zu dieser IMETER-Plattformmethode angegeben: IMETER-Methode N°7 "PUK" sowie zu Theorie und Anwendungen der 'Washburn'-Methode.
13. Spinning Drop, rotating Drop
Aus den geometrischen Maßen eines in einer Flüssigkeit rotierenden Tropfens oder einer Blase wird die Grenzflächenspannung durch eine entsprechende Profilanalyse errechnet. Mit der Methode können sehr geringe Grenzflächenspannungen bestimmt werden.
14. Testtinten (Union Carbide - Methode)
Mit einem Pinsel oder einem besonderen Aufziehgerät, etwa einem Rakel, wird eine Serie standardisierter Flüssigkeiten (Testtinten) in der Reihenfolge ihrer Oberflächenspannungen auf den zu untersuchenden Untergrund aufgebracht. Wenn eine Flüssigkeit nicht mehr benetzt, d.h. nicht binnen 2 Sekunden wieder zusammenfließt, dann entspricht die "Oberflächenspannung" des Feststoffes derjenigen der Testtinte, die zuvorletzt verwendet wurde (einfaches Testverfahren mit praktischer Aussagekraft, doch ohne wissenschaftlichen Anspruch, vgl. Zismann-Verfahren).
DIN 53 364
ASTM D 2578-84
15. Sonstige Methoden
15.a Schwimmende Tropfen: Ein Tropfen schwimmt auf einer anderen Flüssigkeit; Berechnung der Grenzflächenspannung zwischen unmischbaren Flüssigkeiten über die Randwinkel, die die beiden Flüssigkeiten gegeneinander ausbilden.
15.b Schwingender Strahl: Aus einer ovalen Düse strömt Flüssigkeit frei aus einem Behälter. Aus Amplitude und Frequenz des schwingenden Strahls kann die Oberflächenspannung berechnet werden.
15.c Gefrorene Tropfen: Profilanalyse an einem unter Schwerkraft auf nicht benetztem Untergrund erstarrten Flüssigkeitstropfens (z.B. von Metallschmelzen, Gläser); recht ungenaues Verfahren; Auswertung vgl. Methode 8.
15.d Dynamische Lichtstreuung: Laseroptisches Verfahren, wobei statistische Dichte/Temperaturfluktuationen in ihrer Auswirkung bei einer Streulichtüberlagerung zeitaufgelöst analysiert werden. Die Methode erlaubt im Prinzip mehrere thermophysikalische Stoffdaten zu ermitteln: Oberflächenspannung (Oberflächenstreuung), Viskosität (Partikelstreuung), Temperaturleitfähigkeit (molekulare Streuung), Schallgeschwindigkeit u.a.
D. Diskusion zur Messtechnik
Wir stellen selbst Messgeräte für die Ober- und Grenzflächenspannung und die Messung des Kontaktwinkels her. Und haben sowohl aus der Geräteentwicklung und der Erfahrungen aus unseren Dienstleitstungen eine ziemlich praxisorientierte Kenntnis der Wirklichkeit. Wir finden, dass die meisten der vorgenannten Methoden sich wenig für den praktischen Laborgebrauch eignen und die oft nur auf reine Stoffe (ideale Systeme) angewendet werden können. Bei Produkten, Formulierungen, sehr reinen oder reaktiven Stoffen kann die Oberflächenspannung durch Reaktion und Diffusionseffekte beeinflußt werden, so dass ein zeitliche Veränderung der Tension eintritt. Deshalb macht es einen Unterschied wie und wann die Messung erfolgt. Damit die jeweilige Oberfläche zum Zeitpunkt der Messung die Gesamtheit der Flüssigkeit repräsentieren kann, verwenden wir bevorzugt die Ringmethode (mit Rührwerk in temperierter Messzelle und umschlossenem Dampfraum), mit der das Alter der Oberfläche eine kontrollierbare Variable wird. Ebenso sind Temperatur und Stoffkonzentration einfach eingestellte oder kontrollierbare Variablen.
Messen heist vergleichen – über Messprinzipien und Zwecke
Das "Wie" des Messprinzips/der geeigneten Vorrichtung ergibt sich aus Zweck und Ziel: Soll einfach nur die Oberflächenspannung gemessen werden? Genügt ein ungefährer Wert oder soll sie genau oder vor allem einfach bestimmt werden? Sind zeitliche Veränderungen, Wirkungen von Stoffkonzentrationen (z.B. CMC-Bestimmung) und andere Mengen-Wirkungs-Beziehungen, Temperatur- oder Umgebungsabhängigkeiten (Druck, Atmosphäre) von Bedeutung? Sind Resultate des Verfahrens anerkannt? Oder ist für den Zweck, die Messung einer direkten Eigenschaften-Superposition interessanter, da der Anwendung entsprechend? (Etwa, wie bei Geschwindigkeitsabhängigkeiten, also ohne eine Abtrennung anderer physikalischen Einflussgrößen [Viskosität]). Wenn der Zweck der Messung darin besteht, vergleichbare Werte zu bestimmen, sind normierte Verfahren (DIN, ISO, ASTM) unter entsprechend regulierten Umständen anzuwenden. Geht es hingegen um eine Wirklichkeit (d.h. Wirkzusammenhänge), können Abweichungen zum korrekten Messen (z.B. dynamische Messung) auftreten. Gleichwohl sollten die Umstände in Messungen identisch sein, da ohne Vergleichbarkeit dieser, ein Vergleich von Ergebnissen sinnlos ist.
Eine Beschränkung der zur Auswahl stehenden Mittel kann durch die Eigenschaften der Proben vorgegeben werden. Fehlende Transparenz, Empfindlichkeit, Korrosivität des Substrats oder eine höhere Viskosität schließt die Verwendung einiger Methoden aus. Nicht selten sind zeitliche oder durch Mischen veränderliche Werte der Ober-/Grenzflächenspannung an bestimmten Stoffen – oft Formulierungen – zu finden. Was ist dann der wirkliche Messwert?
Selbstverständlich sind nicht alle Messprinzipien/Vorrichtungen im Hinblick auf benötigte Probenmenge, Genauigkeit, Messauflösung und Messbereich vergleichbar. Einschränkende Anforderungen kommen natürlich auch gerade aus dem Umfeld des Einsatzes. In Betriebslabors ist Einfachheit in jeder Hinsicht wichtig, in Forschung/Lehre oder spezialisierten Labors können Messmethoden mehr oder weniger aufwendiger sein, also an die Qualifikation des Prüfers verschieden hohe Anforderungen stellen. Andere Anforderungsschwerpunkte kommen aus dem Zweck z.B. für Serienmessungen oder für Einrichtungen zur Prozessmessung, wo Genauigkeit und Driftstabilität des Messgerätes neben Ausfallsicherheit, Robustheit und Wartungsgünstigkeit noch die lückenlose Dokumentation erfordern. Schließlich muss der apparatetechnische Aufwand der Messvorrichtung selbst und Umstände der Reinigung sowie der Probenzu- und -abführung in Betracht gezogen werden.
Eignung eines Messgerätes prüfen
- Ob ein Gerät den primären Zweck erfüllt: Mist das Gerät richtig? Um diese Grundvoraussetzung eines Messgerätes zu untersuchen, sollten mindestens zwei Referenzflüssigkeiten, die leicht in hoher Reinheit verfügbar sind, gemessen werden (z.B. Hexan und Wasser). Die Resultate sind mit den Sollwerten (Literaturdaten) zu vergleichen. Entsprechendes ist bei anspruchsvolleren Zielvorstellungen wie der Temperaturabhängigkeit zu fordern. Hier soll eine Messung über eine Temperaturänderungen hinweg eine korrekte Reproduktion des Tempertaturkoeffizienten ergeben. Dieses, sofern eine Messauflösung besser als 0.1 mN/m erforderlich ist.
- Ob und wie gut der Zweck erfüllt wird sollte schlicht am beispielhaften Einsatz untersucht werden. Man soll sich nicht Zusätzliche Aspekte können dann in den Vordergrund treten. Nachdem das Ziel des Messgeräteeinsatzes formuliert ist (z.B. QS-Funktionen, Bereiche wissenschaftlicher Fragestellungen, Anwendungsentwicklungen, Optimierungen, Screenings), ist zu prüfen, inwiefern die dazu passende Funktionalität vorhanden und tatsächlich bedienbar ist.
Erlaubt ein Gerät die Prüfung der einzelnen Komponenten, die zur Messung gehören (Temperatur- und Kraftmessung)? Ist Zubehör verfügbar oder ist bei jeder Kleinigkeit der Gerätelieferanten zu kontaktieren? Und der Service: Wieviel? wie oft? wie schnell? wie günstig? auch noch im nächsten Jahr? - Vor Zeiten war nichts anderes von Messgeräten zu erwarten, als dass sie schlicht Messwerte anzeigen. Sie wurden mit den Umständen der Ausführung im Laborjournal notiert. Später hatten Geräte auch Drucker und das Ausgedruckte wurde/wird abgeheftet. Ernsthafte Messgeräte für den Routineeinsatz kommen heute natürlich mit Software. Die muss jetzt dabei sein, zumindest für die Ausgabe von Diagrammen. Wird der Anwender durch weitgehende Automation entmündigt oder genau das nicht? Ob das Gerät eher ein Instrument oder ein Automat ist hängt mit der Qualifikation des Anwenders zusammen und dem Anspruchsniveau der Aufgabe. Muss das unterschieden werden? - Wahrscheinlich steckt in der Behandlung von Ergebnissen (Berechnung, Vergleiche, Statistiken, Archivierung, Konnektivität) das größte unbekannte Potential für die Rationalisierung von Messaufgaben insgesamt. Es ist heutzutage einzufordern, dass Aufgaben wie Dokumentation, Prüfmittelüberwachung, Ergebnisablage in einer LIMS gerechten Form (mit oder ohne eines solchen) durch die Softwarebegleitung erledigt werden.
Entwicklungsmomente von IMETER und die IMETER - Ring-Methoden
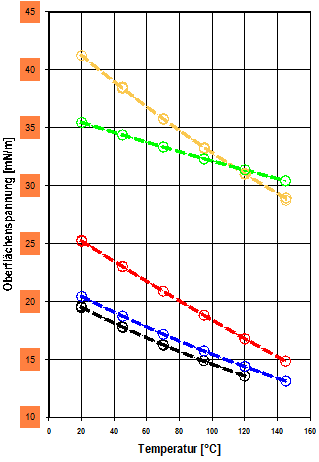
Diagramm 1: Messung der Oberflächenspannung per Ringmethode zwischen 20 und 140°C von Dibenzyltoluol (ocker), einer ionischen Flüssigkeit* (grün), Dodekan (rot), Polydimethylsiloxan (blau) und einem Perfluoralkylether** (schwarz).
* 1-Methyl-1-propylpyrrolidinium bis(trifluoromethylsulfonyl)imide, ** Krytox (R) XHT1000 (DuPont). (Reproduktion mit freundlicher Genehmigung, M. Götz, Karlsruher Instituts für Technologie)
[Allgemeine Ringmethode] Für die allgemeine Messung der Grenz- und Oberflächenspannung darf die Ringmethode (1.) per IMETER als besonders geeignet angesehen werden: Sie kann mit IMETER dynamisch und statisch ausgeführt werden und exakt, schnell und einfach Resultate liefern. Zeitliche Veränderungen und Temperatur- wie Konzentrationseffekte können mit geringem Aufwand gemessen und die Messumgebung kontrolliert auf verschiedene Bedingungen hin angepasst werden. Auch kann die IMETER-Ringmethode für eine weniger anspruchsvolle Bedienung ausgelegt, aber auch in komplexe Zusammenhänge integriert werden. Weiter kannn sie für Regelungsaufgaben und Prozessmessung eingesetzt werden. In Punkto Wiederholgenauigkeit und Langzeitstabilität ist sie auch hier non plus ultra (Drifteleimierung, Justierung in-Process, geschlossene Messzellen).
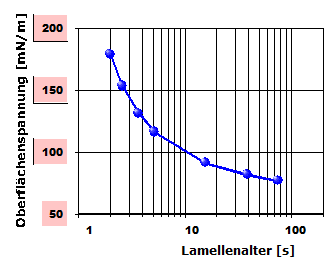
[Statisch - dynamisch] Die Oberflächenspannung ist als thermodynamische Messgröße statisch definiert. Von daher sind dynamische Messmethoden grundsätzlich eher problematisch. Offensichtlich ist der Einfluss der Viskosität (vgl. Diagramm Abb.2). Dynamische Methoden sind tendenziell eher für Vergleichszahlen geeignet.
Bei niedrigviskosen Fluiden und bei moderater Mess- bzw. Abzugsgeschwindigkeit wird normalerweise keine Abweichung zu einer rein statischen Messweise gefunden. "Statisch" bedeutet, dass der Lamellenauszug in stufenweise z.B. in langsamen Bewegschritten erfolgt, wobei solange gewartet wird, bis sich die am Ring wirkende Kraft nicht mehr ändert. Es ist aus vielen Gründen besser, nach unserem Patent (DE 4412405) zu verfahren, als eine sehr langsame dynamische Zuggeschwindigkeit anzuwenden. Andernfalls bräuchte eine Messung sehr lange, der Messwertzeitpunkt (Lamellenalter) könnte kaum zugeordnet und zeitliche Effekte nicht richtig angezeigt werden (Diffusion) oder sogar die Messung stören (Drift).
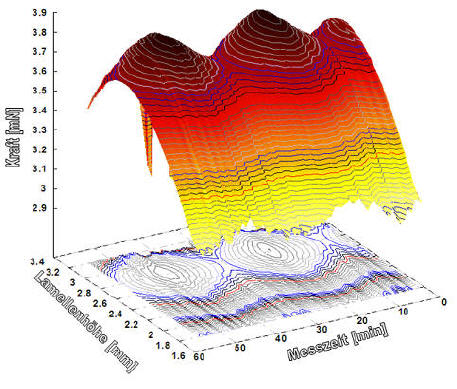
Abb. 2: "Oberflächenspannung " von Honig. Darstellung in Abhängigkeit von der Messgeschwindigkeit. Diese wird von der Software als Lamellenalter in dem automatisch erzeugten Diagramm dargestellt (=> durch Viskositätseinfluss ohne Gleichgewichtseinstellung der Kräfte zu einer 'Viskosispannung').
Gegenüber der Methode des hängenden Tropfens (Pendant Drop, 6.) muss der Ringmethode ein verfahrensbedingt größerer Messfehler zugeordnet werden. Sie setzt jedoch bei der Messung der Grenzflächenspannung keine Durchsichtigkeit voraus. Änderungen des Brechungsindex durch Temperatur oder Stoffumsatz spielen bei der Ringmethode keine Rolle. Hingegen liefert sie Zusatzinformationen (z. B. Lamellenhöhe) und die Dokumentation erlaubt an den Messkurven Fehlmessungen ggf. nachträglich als solche zu erkennen. Konzentrationsbedingte Grenzflächenphänomene, zeitliche und thermische Effekte werden messtechnisch sehr einfach zugänglich gemacht, auch echte Mittelwerte, die man anders kaum erhält. Die "Ablesung" ist außerdem automatisiert, unkomplizierter, einfacher und sicherer und hat auch keinen Benutzerfaktor.
In Abb. 3 ist die zeitliche Entwicklung der Grenzflächenspannung zwischen Wasser und Toluol dargestellt. Das Beispiel zeigt, wie einfach zeitliche Effekte dokumentiert werden können; von selbst nämlich. - Die Grenzflächenspannung wird normlerweise an den gegenseitig gesättigten Phasen bestimmt. Im Beispiel also toluolgesättigtes Wasser gegen wassergesättigtes Toluol. Mit der Steuerung und Auswertung von IMETER kann unter Einsatz von ►I-Magnetrührer das gesamte Phasenverhalten in einem Messablauf bestimmt werden.
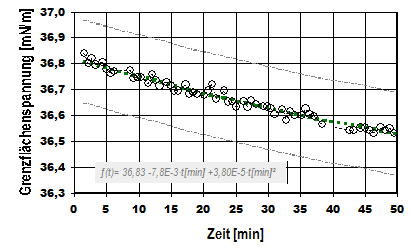 Abb. 3: Die frische Grenzflächenspannung zwischen Wasser und Toluol beobachtet über 50 Minuten (25.0°C): Die Grenzflächenspannung nimmt im Verlauf um 0.3 mN/m ab. [5103]
Abb. 3: Die frische Grenzflächenspannung zwischen Wasser und Toluol beobachtet über 50 Minuten (25.0°C): Die Grenzflächenspannung nimmt im Verlauf um 0.3 mN/m ab. [5103]
[Nullpunktsdrift ] Die Streuung der einzelnen Messwerte wird wegen der geringeren Messunsicherheit verursacht. Das klingt zunächst paradox, "höhere Sicherheit durch größere Streuung"! Es ist also so: jeder einzelne Messpunkt entspricht einer Bestimmung der Maximalkraft (vgl. Diagramm 1). In dieser Messung wurde vorgegeben, jeden einzelnen Messwert mit seiner eigenen Bezugskraft auszustatten. Für einen Oberflächenspannungswert wurden somit zwei Wägungen vorgenommen, was die Präzision (Precision) durch Streuung verschlechtert, doch die Richtigkeit (Accuracy) und Sicherheit verbessert. Durch die Technik der Bezugskraftbestimmung ist es kein Problem, wenn ein Tröpfchen an der Ringhalterung sich niederschlägt oder der Nullpunkt der Wägezelle aus anderen Gründen driftet. Der Fehler korrigiert sich durch die Bezugskraftmessung von selbst, also per kurzzeitiger Kraftdifferenzmessung.
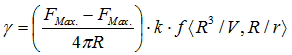 (Ring-Gleichung)
(Ring-Gleichung)
Fmax. (Maximalkraft bei Auszug der Lamelle), FBez. (Bezugskraft), R (Ringradius), r (Ringdrahtradius), k (Ringkorrektur), f (Korrekturfaktor je nach Berechnungsalgorithmus, Ringgeometrie und gehobenem Flüssigkeitsvolumen V).
(Anmerkung zur Bezugskraftbestimmung: der Ring ist dabei um eine vorgegebene Strecke mit rückwärtigen Meniski an den Halteschenkeln eingetaucht (dies sollen Anwender aus den Standardmessprogrammen beibehalten). Der Ringauftrieb und die Wilhelmy-Oberflächenspannung [rekursiv] an den Schenkeln wird berechnet, so dass die Bezugskraft für den frei hängenden Ring aus den bekannten Daten berechnet wird. Zusätzlich: Die Ringgeometrie wird über die thermische Wärmedehnung des Ringmaterials korrigiert, was bei normalen Temperaturen zwar keine Rolle spielt - es ist ja geradezu ein Dogma der IMETER-Software, die Korrektheit grundsätzlich einzubauen, schließlich kann IMETER mit einer Mikrowaage ausgestattet sein oder es wird bei extremen Temperaturen gemessen; Ringdimension und Material sind ebenfalls nicht festgelegt.)
Daneben kann für Prozessmessungen auch die In-Process-Justierung eingesetzt werden, die die Justierung der automatisch Wägezelle durchführt (z.B. auf der Ebene der Ablaufsteuerung ausgelöst durch eine Temperaturänderung an der Wägezelle).
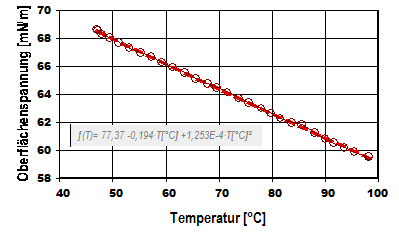
Abb. 4: Oberflächenspannung einer Wasserprobe bei Messungen zwischen 50 und 98°C (mit automatisch erzeugter "Formel").
Mehrfachbestimmungen, wie die gezeigten, sind beispielsweise mit der Wilhelmy-Platte (Methode 2.) nicht möglich. Praktisch bietet diese Möglichkeit nur die Ringmethode. Und die Ringmethode hat gegenüber der Wilhelmy-Platte noch den Vorteil, dass konkurrierende und asymmetrische Adsorptionsvorgänge (Benetzungsstörungen) kaum auftreten können.
Grundlegende Verhältnisse können anschaulich illustriert werden: Das Diagramm (rechts) visualisiert die Rohdaten (Kraft, Lamellenhöhe, Zeit) bei andauernder Messung der Oberflächenspannung an Toluol mit der Ringmethode. Die Temperatur ändert sich linear auf- und absteigend, dreimalig zwischen 20 und 30°C, wodurch sich die Oberflächenspannung entsprechend verändert (►Dauermessung an Toluol.PDF).
Abb. 5 (rechts): temperierte hohe Doppelkammer-Messzelle mit Magnetrührwerk.

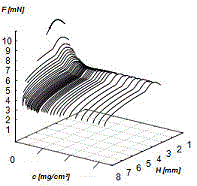
►CMC-Messung - mit beabsichtigtem Lamellenabriss (bereits eine minimale Tensidmenge stabilisiert die Lamelle). Was keinen Regelfall markiert, denn bei einem anderen Tensid konnten stabile Lamellen nur im Bereich der CMC gefunden werden.
► Zur phänomenologischen Betrachtung und Festkörpermessungen ...