IMETER - Methode N°7 "PUK"
Herleitung, Tests, Ergänzungen und Materialien
| 1. Herleitung |
| 2. Weiterentwicklung |
| 3. Simulation, Test & Korrekturen |
| 4. Sorptivität, Porosität, Partikeloberfläche |
| 5. Probenformen |
| 6. Entwicklungsthemen |
 M7 / PUK-Messung von Pulvern im IMETER Messgerät: Die Probe befindert sich in einer Glasröhre innerhalb der temperierten Messzelle. (Eine Volumenfixierung der Probenröhre verhindert die Expansion der Probe im Verlauf der Messung).
M7 / PUK-Messung von Pulvern im IMETER Messgerät: Die Probe befindert sich in einer Glasröhre innerhalb der temperierten Messzelle. (Eine Volumenfixierung der Probenröhre verhindert die Expansion der Probe im Verlauf der Messung). Sie finden hier wesentliche Details zur ♦ IMETER-Methode N7 PUK ausgeführt. Eine Herleitung und Weiterentwicklung der Washburngleichung, Simulationen mit Experimentaldaten, Sonderfälle und Anwendungsbeispiele zur Sorptivität und die Anwendbarkeit bei verschiedenen Probenformen wird vorgestellt. Diese Seite ist Originalquelle mehrer Neuheiten - zu Theorie, Anwendung und über apparative Verbesserungen. Angemeldete Besucher können sich anhand ♦ der Anleitung von der Einfachheit der Messung überzeugen.
- Quellenangabe: IMETER M7 von Michael Breitwieser und Thomas Petzoldt -
Herleitung und Weiterentwicklung der Washburn Gleichung
1. Herleitung
[Grundlagen] Die so genannte Washburn-Gleichung wird zur Beschreibung des Zeitgesetzes für das Eindringen einer Flüssigkeit in ein poröses Material verwendet. In der Modellvorstellung wird der poröse Stoff als Kapillarenbündel aufgefasst, in das die Flüssigkeit entsprechend der Benetzungsverhältnisse und der Viskosität aufgenommen wird. Die Washburn-Gleichung basiert auf einer Zusammenführung des Hagen-Poiseuille'schen Gesetzes mit der Young-Laplace-Gleichung.
Das Fluidvolumen (Volumenstrom V·), das durch eine Röhre der Länge h strömt, entspricht direkt dem Druckunterschied Δp und ist umgekehrt proportional zur Viskosität η des strömenden Fluids und der Röhrenlänge h; dabei wächst das Durchflussvolumen in vierter Potenz mit dem Röhrenradius r.
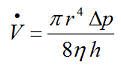 Gl.1 (Hagen - Poiseuille 1839)
Gl.1 (Hagen - Poiseuille 1839)
Der Volumenstrom V· kann für ein Rohr auch über die differenzielle Strömungs- bzw. Steiggeschwindigkeit dh/dt pro durchströmter Fläche (πr²) der Röhre oder Kapillare ausgedrückt werden. Da V· = dV/dt = πr ²·dh/dt ergibt sich mit Gl.1:
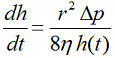 Gl.2
Gl.2
"Die Steiggeschwindigkeit dh/dt in einer Kapillaren folgt dem antreibenden Druck Δp, der jedoch durch die Viskosität η und die bereits zurückgelegte Strecke h(t) gehemmt wird."
Die antreibende Druckdifferenz Δp in einer Röhre ist eine Folge der Benetzung der Röhrenwand. Die Benetzung verformt die Flüssigkeitsoberfläche konkav und ein Druck entsteht durch die Oberflächenspannung γ der Flüssigkeit.
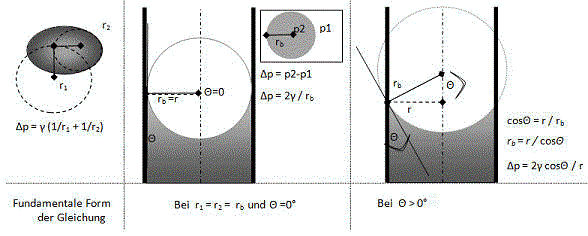
Abb. A: Young-Laplace-Gleichung: <Links> Über einer beliebig gekrümmten Oberfläche ist der Druck (d.h. die Druckdifferenz über der Oberfläche) durch die Oberflächenspannung und die Hauptkrümmungsradien r1, r2 festgelegt. <Mitte> Bei r1=r2=r (Kugel), entsprechend Θ=0°, ist der Druck Δp=2γ/r; <rechts> Wenn der Randwinkel Θ nicht 0° beträgt, ist der wirkende Druck im Meniskus gegeben durch Δp=2γ cos(Θ)/r. (Bei Θ=90° ist die Fluidoberfläche plan, r1, r2 → ∞ also Δp=0; bei Θ>90° ist die Oberfläche konvex und damit Δp < 0, d.h. Kapillardepression)
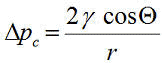 Gl.3 (Young - Laplace 1805)
Gl.3 (Young - Laplace 1805)
[Washburn-Gleichung] Setzt man Gl.3 in Gl.2 ein , ergibt sich die Steiggeschwindigkeit in einer Röhre:
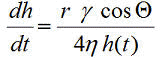 Gl.4
Gl.4
Die Gl.4 wird integriert:
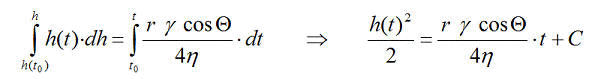 Gl.5
Gl.5
Man erhält die landläufige Form der Lucas-Washburngleichung[2,3,4,1]
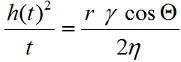 bzw.
bzw. 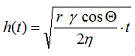 Gl.6 (Washburngleichung 1921)
Gl.6 (Washburngleichung 1921)
Die Washburngleichung gilt eigentlich für waagerecht liegende Kapillaren – statt "h" Steighöhe wäre daher "l" für Infiltrationsstrecke das geeignetere Symbol. Bereits bei nicht sehr feinporigen Materialien – gleichbedeutend mit Pulverpräparaten aus Partikeln mit Durchmessern um 20 µm – ist der Druck (Gl.3) bereits bei mäßiger Benetzung so groß, dass Steighöhen im Meterbereich auftreten. Die Gegenkraft, die bei der vertikal aufsteigenden Infiltration durch die Flüssigkeitssäule entsteht, also der hydrostatischer Druck - er wird weiter unten thematisiert, ist bei den typischen Messungen mit Probenhöhen im unteren Zentimeterbereich meistens oh Infiltration einer Flüssigkeit in ein Pulver (das Röhrchen ist unten durch eine G0-Glasfritte begrenzt).ne Bedeutung.
Infiltration einer Flüssigkeit in ein Pulver (das Röhrchen ist unten durch eine G0-Glasfritte begrenzt).ne Bedeutung.
Die IMETER-Methode N°7 "PUK" stellt gravimetrische Verfahren zur Messung von Infiltrationsmengen und Geschwindigkeiten einer Flüssigkeit in poröse Materialien bereit. Wie kann nun das gravimetrische Messprinzip hier angewendet werden, um eine Gewichtszunahme in Steighöhe umzuwandeln?
[Modifizierte Washburngleichung] -- Die Umformung des Zusammenhangs von Steighöhe auf Gewichtszunahme läuft bisweilen unter dem Begriff "modifizierte Washburn-Gleichung"[5]. Die Kapillaren werden weiterhin als Bündel gerader Kreiszylinderröhren gedeutet. Die Gewichtszunahme durch die Masseinfiltration substituiert jedoch die Steighöhe h durch Steigvolumen. Da in der Realität gerade Kreiszylinderröhren praktisch gar nicht vorkommen, bietet letztendlich die gravimetrische Messung der Infiltration die tatsächlich korrekte Verbindung zur Theorie. Denn die Washburn-Gleichung bringt ja nicht Steigstrecken sondern Volumenströme (aus ihrer Hagen-Poiseuille'schen Herkunft) mit Kapillarität und Viskosität ins Gleichgewicht. Steighöhen oder -Strecken sind für alle Fälle, bei welchen nicht exakte Zylinderröhren vorliegen, ein ungeeigneter Ansatz. Die gravimetrische Formulierung hingegen, ist universell und auch für den Spezielfall von Zylinderröhren anwendbar. Gleichwohl, für die Formulierung des Modells bieten Steigstrecke und -geschwindigkeit in Röhren den Lösungsansatz, der sich wie folgt herleitet:
Dem gesamten Kapillarenvolumen V in einem Material entspricht:
V = r²·π·h·n
Dabei ist „r²·π·h“ das Volumen einer und n die Anzahl aller Kapillaren. Das Volumen V ist dasjenige Volumen im porösen Stoff, das anfangs leer ist und durch die aufsteigende Flüssigkeit eingenommen wird. Mittels der Dichte der Flüssigkeit (ρ) wird das Volumen durch die Masse (m) ersetzt:
m / ρ = r²·π·h·n
Nach der Höhe bzw. Länge h einer Kapillare umgestellt
h = m /( ρ·r²·π·n)
und entsprechend „h²/t“ für die Washburn-Gleichung quadriert:
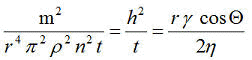 Gl.6A
Gl.6ADie Gleichung 6A kann aufgeteilt werden in links, den Teil, der gravimetrisch direkt gemessen werden kann, und rechts, den Teil, was aus Konstanten der Flüssigkeit zugänglich ist sowie dem Unbekannten in der Klammer.
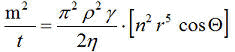 Gl.6B
Gl.6BDas Produkt n2r5 wird als Materialkonstante (K) bezeichnet. Erfolgt die Messung mit einer Flüssigkeit, die das Probenmaterial total benetzt, d.h. cos Θ = 1, dann kann K nach folgender Gleichung ermittelt werden:
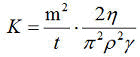 Gl.6C
Gl.6CFalls der Kontaktwinkel Θ durch Literaturdaten oder Messung an kompakten Materialproben (►IMETER M4) bekannt ist, kann K auch unter dieser Vorgabe berechnet werden. Die Materialkonstante K kann bei weiteren Messungen mit anderen Fluiden eingesetzt werden, um jeweilige Kontaktwinkel zu bestimmen und schließlich die Bestimmung der Oberflächenenergie des Materials erlauben.
[Gewicht in Steighöhe] Zurück zum Ausgangspunkt der Steighöhe: Die Infiltrationsmenge d.h. die Steighöhe wird also aus den Wägedaten bestimmt. Wie geht das? Die infiltrierte Weglänge, d.h. die Probenhöhe und die final aufgenommene Fluidmenge definieren Eckpunkte eines Vorgangs, der sowohl am Anfang als auch am Ende der Flüssigkeitsaufnahme durch andere Effekte überprägt ist (vgl. oberes Diagramm rechts). Regulär ist der Bereich, für den die Differenzenquotienten aus quadrierter Aufnahmemenge gegen die Zeit einen konstanten Wert aufweisen (Δm²/Δt=const.), d.h. ein konstantes K haben. Hier ist der Vorgang stationär und konform mit der Theorie. Der stationäre Sorptionsstrom stellt sich am Beginn also erst nach einer gewissen Vorlaufzeit bzw. Infiltrationsstrecke ein. Und am Ende tritt auch kaum ein abrupter Stopp des Vorgangs auf, weil die Kapillaren i.d.R. uneinheitlich sind, schnelle Pfade die Oberfläche bereits erreicht haben, doch seitliche Ausbreitungsbewegungen und auch Einzüge in weniger zugängliche Bereiche auftreten, die die Infiltration gebremst abklingen lassen. - Aus dem linearen Bereich der roten m²/t-Kurve (rechts, unteres Diagramm) wird durch Extrapolation der Zeitpunkt des Erreichens der finalen Infiltrationsmenge bestimmt. Zu diesem Zeitpunkt würde eine regulär fortgesetzte Infiltration die Probenhöhe erreichen (wenn keine Probenenden-Efekte aufträten) - und genau damit ist der Streckenbezug der gravimetrischen Messung hergestellt.
Optisch gemessene Steighöhen können eher nicht zur Parametrierung der Washburn-Gleichung herangezogen werden. Es gibt Indikationsschwierigkeiten und die Ablesung der Steigstrecke wird auch dadurch verfälscht, dass schneller entlang der Probe aufsteigenden Fließfronten dominieren, während Anteile, die verzögert in weniger gut zugängliche Hohlräume und lateral einziehen und nicht erfaßt werden; Damit aber wird die Voraussetzung der Washburn-Gleichung ausgehebelt - denn sie basiert ja nicht auf Steighöhen oder -Strecken sondern auf tatsächlich fließenden Volumentströmen. Nur über den stattfindenden Flussigkeitstransport kann ein effektiver Kapillarradius angesetzt werden, der das poröse Material charakterisiert.
Die Kenntnis der tatsächlicher durchflossenen Kapillarweglänge ist für die formale Behandlung wie gezeigt evident. Aber besonders in Haufwerken bzw. Pulverschüttungen ist diese Größe kaum einschätzbar. Das Verhältnis von tatsächlichen Fließpfadlänge zu geometrsich kürzester Verbindung (gerade Linie) - wird Tortuosität genannt - könnte mit h entsprechend korrigiert, bessere Schätzungen für r und die anderen Ableitungen ermöglichen.
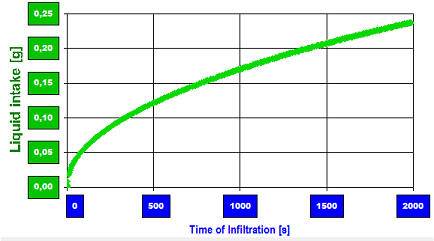
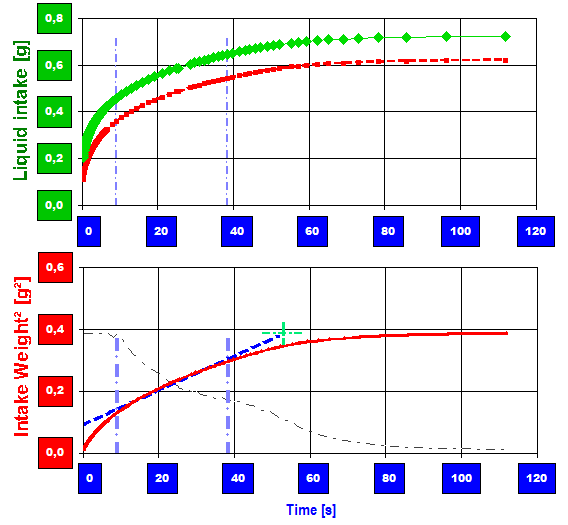
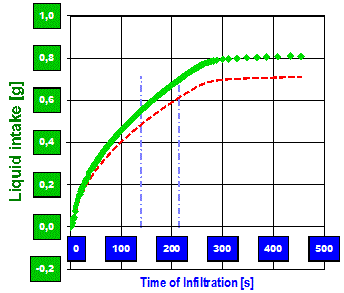 PTFE-Mikropulver in einem Frittenröhrchen, Infiltration von n-Oktan: Die grünen Marken zeigen den Verlauf der Infiltration anhand der Gewichtszunahme an. - Nach Kontakt des PTFE-Pulvers mit Oktan wird dieses hochgezogen; damit steigt das Gewicht durch die Infiltration an. Nach ca. 300 Sekunden hat die Fließfront die Probenoberfläche erreicht, die Flüssigkeitsaufnahme beendet sich und die Kurve knickt waagerecht ab. Die rote Linie repräsentiert das in die Probe aufgenommene Nettogewicht m der Flüssigkeit (nach Berücksichtigung der Auftriebskorrektur); die blauen Baken markieren den Zeitbereich der Messung, der in der mathematischen Auswertung untersucht wird. Siehe nachfolgendes Bild.
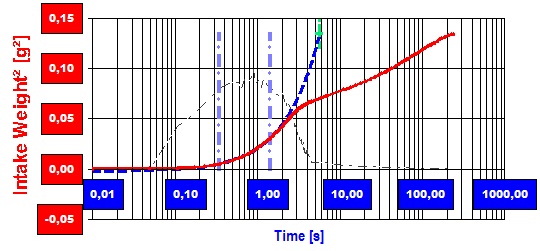
PTFE-Mikropulver in einem Frittenröhrchen, Infiltration von n-Oktan: Die grünen Marken zeigen den Verlauf der Infiltration anhand der Gewichtszunahme an. - Nach Kontakt des PTFE-Pulvers mit Oktan wird dieses hochgezogen; damit steigt das Gewicht durch die Infiltration an. Nach ca. 300 Sekunden hat die Fließfront die Probenoberfläche erreicht, die Flüssigkeitsaufnahme beendet sich und die Kurve knickt waagerecht ab. Die rote Linie repräsentiert das in die Probe aufgenommene Nettogewicht m der Flüssigkeit (nach Berücksichtigung der Auftriebskorrektur); die blauen Baken markieren den Zeitbereich der Messung, der in der mathematischen Auswertung untersucht wird. Siehe nachfolgendes Bild.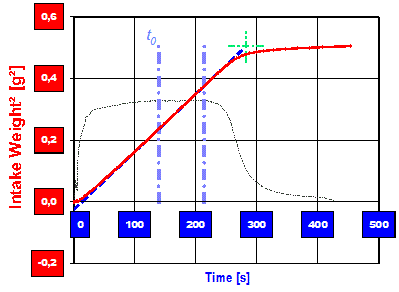 Die rote Linie gibt hier die nun quadrierte Aufnahmenge (m²) gegen die Zeit (t) wider. Ihre Steigung m²/t entspricht der Aufnahmegeschwindigkeit des Fluids und ist gemäß der Herleitung mit Gl.6B eine Konstante. Um einfacher erkennen zu können, wo und über welchen Zeitbereich die Sorption gesetzmäßig verläuft, wird zusätzlich der Differenzenquotient Δm²/Δt als grau gestrichelte Linie im Dagramm eingetragen. Die beiden Baken markieren also einen Zeitbereich mit konstanter Infiltrationsgeschwindigkeit.
Die rote Linie gibt hier die nun quadrierte Aufnahmenge (m²) gegen die Zeit (t) wider. Ihre Steigung m²/t entspricht der Aufnahmegeschwindigkeit des Fluids und ist gemäß der Herleitung mit Gl.6B eine Konstante. Um einfacher erkennen zu können, wo und über welchen Zeitbereich die Sorption gesetzmäßig verläuft, wird zusätzlich der Differenzenquotient Δm²/Δt als grau gestrichelte Linie im Dagramm eingetragen. Die beiden Baken markieren also einen Zeitbereich mit konstanter Infiltrationsgeschwindigkeit. 2. Weiterentwicklung der Washburn-Gleichung
Die Korrektheit der Washburn-Gleichung ist vielfach bestätigt[6] und sie wird seit langer Zeit angewendet, beispielsweise auch bei der Quecksilber-Porosimetrie [79, S.335-338]. Washburn bietet eine vergleichsweise einfach handhabbare Beschreibung ziemlich komplexer Vorgänge. Bei der Anwendung in einer exakten Messtechnik kann die Formel gleichwohl nur selten unmittelbar angewendet werden. Denn oft bildet sich im porösen Material die geschlossene aufsteigende Flüssigkeitsfront erst nach einer gewissen Zeit und nicht bereits ab dem Zeitpunkt Null (vgl. Beispiele unten auf dieser Seite).
[Korrektur in der traditionellen Berechnung] Da sich ein stationärer Zustand, den die Gleichung beschreibt, mehr oder weniger verzögert einstellt, ist die Dauer zur Ausbildung desselben (Latenzzeit) formal zu behandeln. Die Washburn Gleichung bietet diese Möglichkeit, einfach, indem sie richtig ausgerechnet und angewendet wird. So beginnt unsere Weiterentwicklung hier zuerst mit der Korrektur von Fehlern, die in Praxis und Literatur verbreitet sind und zusammen mit mangelhaften Ausführung der Messungen selbst, dazu führen, dass das Potenzial die Methode dort unausgeschöpft bleibt. - Eine Latenzzeit kann formal dadurch berücksichtigt werden, dass ein Auswertungsbereich (vgl. Diagramm oben) so festlegt wird, dass die Berechnung eben nur den Bereich regelrechter Werte umschließt. Dabei wird die Integrationskonstante (t0) als Bezugszeit festgelegt, ab der die Washburngleichung berechnet wird. Die Bestimmung der Integrationskonstanten "C" erfolgt nach Gl.5, mit "C= h (t0)2 / 2 - r y cosΘ t0 / 4η". Daraus ergibt sich:
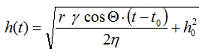 Gl.7
Gl.7
Ein Mangel der Washburngleichung ist, dass sie unendlich das √t-Gesetz fortsetzt, also kein Ende des Aufsteigens erreicht würde. Wie die trockene Erde über Grundwasser, Schluff und Sand am Strand beweisen, steigt das Wasser in pöroser Materie nicht unbegrenzt weit nach oben.
[Berücksichtigung der Schwerkraft] Der antreibende Druck Δp in Gl.2 muss also dem ziehenden Kapillardruck pc entgegenwirkende Beiträge enthalten:
Δp = Δpc - ph - pd ± Δpa ± ... Gl.8
(pc Laplace- oder Kapillar-, ph hydrostatischer, pd Verdrängungs-, pa externer, ... Druck)
Mit dem Aufsteigen der Flüssigkeit wächst die Flüssigkeitssäule empor. Damit wächst der viskositätsbedingte Reibungswiderstand. Und entsprechend der Steighöhe nimmt das Gewicht Dichte-, Gravitations- und Steighöhenproportional zu. Der Druck, der durch die Höhe der Flüssigkeitssäule ausgeübt wird, ist ihr Schweredruck, d.h. der hydrostatische Druck ph.
ph = Δρ g h (t) Gl.8A
(ρ Dichte der Flüssigkeit bzw. Δρ die Dichtedifferenz im gemeinsamen Medium; g für die Schwerebeschleunigung)
Entsprechend in Gl. 2 eingesetzt, ist demnach zu schreiben:
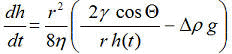 Gl.9
Gl.9
Der Ansatz muss richtig sein, denn aus dieser Formulierung ergibt sich direkt Jurin's Gesetz – die maximale Steighöhe in Kapillaren – indem hier einfach die Bedingung dh/dt=0 gesetzt wird. D.h. wenn dh/dt=0 eintritt, findet kein weiteres Aufsteigen statt. Der Kapillardruck ist dann gleich dem hydrostatischen Druck und die erreichte Steighöhe h(t) ist hfin die finale, bzw. die maximal erreichbare Steighöhe:
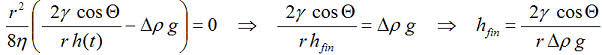 Gl.9a (Jurin-Gleichung)
Gl.9a (Jurin-Gleichung)
Die Lösung der Differenzialgleichung Gl.9 ergibt:
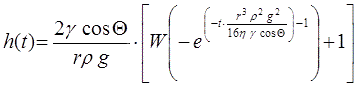 Gl.10
Gl.10
('W' steht für die Omega-Funktion).
[Verdrängungsdruck] Es gibt noch einen Faktor, der als wirksame Druckkomponente bei seitlich eingeschlossenen Proben berücksichtigt werden sollte: nämlich der dynamische Gegendruck bzw Verdrängungsdruck . - Bei Messungen mit Pulvern in Frittenröhrchen besonders an feinen und dicht gepackten Pulvern kann beobachtet werden, dass Gasblasen durch den Boden des Frittenröhrchens ausgepresst werden, bevor sich die geschlossene Fließfront bildet. Die aufsteigende Flüssigkeit verdrängt die Luft, die anfangs, dem Druckgradienten folgend, nach unten ausgepresst wird. Wie beim hydrostatischen Druck, der bei guter Kapillarität im Setup der Messungen oft keine Rolle spielt, so ist auch der Verdrängungsdruck eher eine Ausnahmeerscheinung. Doch sollte ein möglicher Effekt kalkulierbar sein. Denn, immerhin es ist zu beachten, dass bei 20°C die Viskosität von Luft ~0,02 mPa·s beträgt; Hexan hat 0,32 mPa·s. Damit ist der Kohlenwasserstoff (nur) rund 15x viskoser. Bei mikro- bis mesoporösen Materialien (Poren < 2 nm bis 50 nm) kann ein Effekt unbedingt erwartet werden. Die Situation ist ähnlich, wenn eine Flüssigkeit in einem porösen Gefüge durch eine besser benetzende Flüssigkeit verdrängt wird, z.B. wenn ein wässriges Medium Mineralöl aus porösen Lagerstätten austreiben soll.
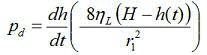 Gl.11
Gl.11
Der Verdrängungsdruck pd wird entsprechend dem Hagen-Poiseuilleschen Gesetz (Gl.2) angesetzt. Je größer die Steiggeschwindigkeit und Probenhöhe und je höher die Viskosität ηL des zu verdrängenden Fluids ist, desto stärker wirkt die Viskosität des zweiten Mediums quasi als sich dynamisch verringernder Gegendruck. Der Term "H-h(t)" ist die Pegelhöhe aus der das Fluid verdrängt wird; H ist die gesamte Höhe der Probe (bzw. die Kapillarlänge). Am Ende der Infiltration ist h(t)=H. Diese Druckkomponente wird im Verlauf also immer kleiner und verschwindet schließlich, wohingegen der hydrostatische Druck zunimmt. Die komplette Differenzialgleichung dazu:
[BP-Gleichung]
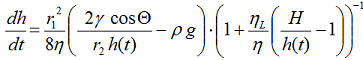 Gl.12
Gl.12
Als weitere Schikane wird in Gl.11 und 12 der Kapillarradius r durch r1 und r2 ersetzt. Zwei verschiedene Kapillarradien einzusetzen hat sich inzwischen als fruchtbare Option zur Annäherung an Wirklichkeit erwiesen. Z.B. wenn das poröse Material als Kugelpackung angesehen wird – diese ist dem Normalfall zweifellos ähnlicher, als ein Material, das aus geraden Kreiszylinderröhren besteht –, dann darf auch angenommen werden, dass es nicht nur mittlere Kapillarradien r, sondern mittlere Minimalradien r1 und mittlere Maximalradien r2 gibt. Es ist aus den kinematischen Grundlagen einsichtig, dass der Kapillardruck durch die größten auftretenden Radien im Kapillarsystem begrenzt wird (Laplace-Radius r2), wohingegen Engstellen den Viskositätseinfluss dominieren (Hagen-Poiseuille-Radius r1). Diese Situation ist in der Abb. rechts schematisch dargestellt.
Mit dem Ansatz r = r1²/r2 bleiben die ursprünglichen Verhältnisse der Washburngleichung jedenfalls solange gewahrt, wie die Hydrostatik unbedeutend ist.
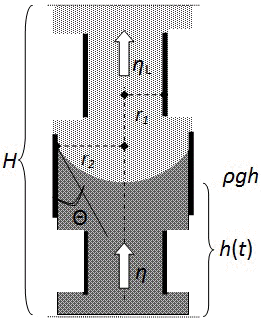 Laplace-Kapillardruck, hydrostatischer Druck, viskoser Gegendruck ... Das Modell skizziert, dass der Druck durch den maximalen Holraumradius r2 und die Flussrate durch die Engstellen r1 begrenzt. Für die maximale Steighöhe ist r2 verantwortlich.
Laplace-Kapillardruck, hydrostatischer Druck, viskoser Gegendruck ... Das Modell skizziert, dass der Druck durch den maximalen Holraumradius r2 und die Flussrate durch die Engstellen r1 begrenzt. Für die maximale Steighöhe ist r2 verantwortlich. Die Lösung der Differenzialgleichung Gl.12 ergibt mit Gl.13 einen leider recht komplexen Term:
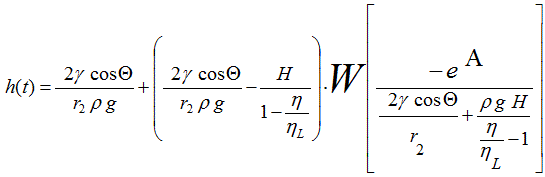 Gl.13 (BP-Gleichung)
Gl.13 (BP-Gleichung)
In der Gleichung bedeutet "W " die Lambert-W-Funktion (vgl. Abb.); der Wertebereich ist W ≥ -1.
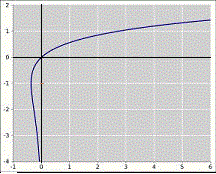 Abb. Verlauf der Lambert-W-Funkt ion (Lambertsche-W- oder Omega-Funktion; d.i. die Umkehrfunktion von y=xex)
Abb. Verlauf der Lambert-W-Funkt ion (Lambertsche-W- oder Omega-Funktion; d.i. die Umkehrfunktion von y=xex)
Der Ausdruck A - der Exponent - enthält die Variable t und wird gebildet durch ...
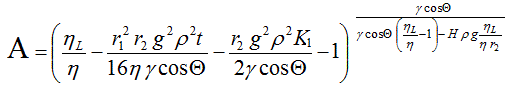
K1 ist die Integrationskonstante (t0 Startzeit; h0 Steighöhe zur Zeit t0)
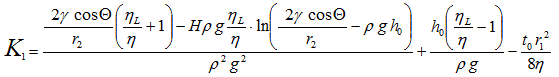
Mit ηL=0 wird der Term durch den Ausfall entsprechender Glieder einfacher; es wird dann nur der hydrostatische Druck berücksichtigt. So kann die Gleichung auch für Probenmessungen verwendet werden, bei welchen ein Druckausgleich nicht durch die Probenmasse erfolgt (Proben ohne Röhrchen, kompakte Proben, Textilien). An der Lambertschen W-Funktion kommt man auch bei der Lösung der entsprechend einfacheren Differenzialgleichung nicht vorbei, also selbst wenn nur Gl.9. integriert wird. -- Die Gl.13. bezeichnen wir als Universal- oder "BP-Gleichung".
[Bosanquet] Im Rahmen der Überprüfung und auf der Suche nach vielleicht besseren Lösungen kam die sog. Bosanquet-Gleichung [14, 15] in Betracht:
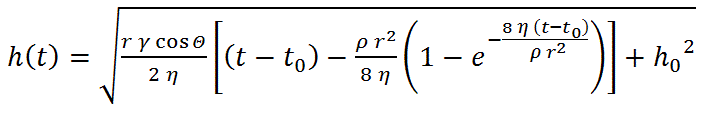 Gl. 14
Gl. 14
Gl. 15 präsentiert in expliziter Form und mit den oberhalb eingeführten Symbolen die Gleichung so, wie wir sie auch 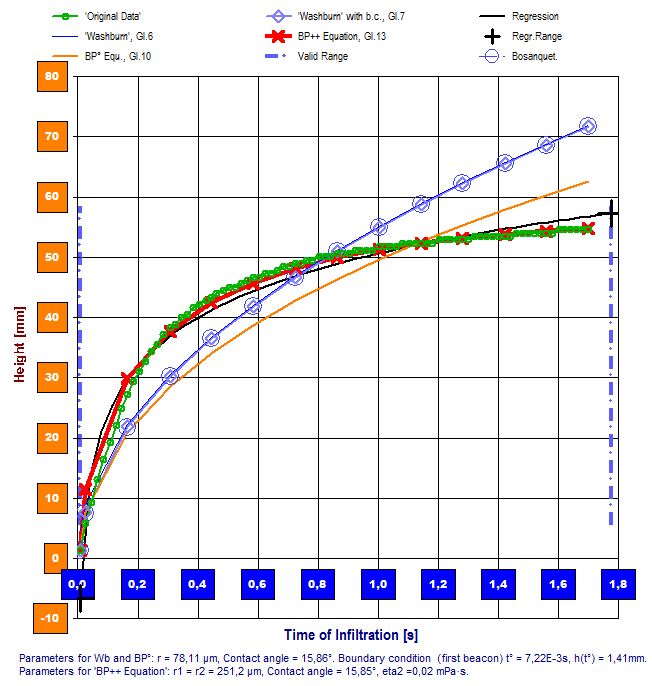 Einsatz der Gleichungen zur Beschreibung der Kapillardynamik und Steighöhe: Vgl. Test Washburn/Kapillar-Flussexperiment mit einer einzelnen Kapillare (PDF). zur Prüfung eingesetzt haben. Im Gegensatz zur Washburn-Gleichung, die auf Geschwindigkeit basiert, fusst die Bosanquet-Gleichung auf Beschleunigung, was bei Wirkung von Kräften sehr plausibel ist. Für unsere aktuell verfügbaren Ausrüstungen sind Untersuchung der Zeiträume von unter 0.02 Sekunden nach Flüssigkeitskontakt nicht zugänglich und praktisch ohne Bedeutung. Zu Vorgängen, die etwa ab 0.05 Sekunden nach Kontakt auftreten, können wir konstatieren, dass die Bosanquet-Gleichung stets promillegenau die selben Resultate liefert wie die Washburn-Gleichung (Gl.7).
Einsatz der Gleichungen zur Beschreibung der Kapillardynamik und Steighöhe: Vgl. Test Washburn/Kapillar-Flussexperiment mit einer einzelnen Kapillare (PDF). zur Prüfung eingesetzt haben. Im Gegensatz zur Washburn-Gleichung, die auf Geschwindigkeit basiert, fusst die Bosanquet-Gleichung auf Beschleunigung, was bei Wirkung von Kräften sehr plausibel ist. Für unsere aktuell verfügbaren Ausrüstungen sind Untersuchung der Zeiträume von unter 0.02 Sekunden nach Flüssigkeitskontakt nicht zugänglich und praktisch ohne Bedeutung. Zu Vorgängen, die etwa ab 0.05 Sekunden nach Kontakt auftreten, können wir konstatieren, dass die Bosanquet-Gleichung stets promillegenau die selben Resultate liefert wie die Washburn-Gleichung (Gl.7).
[Prüfung der Grundlagen]
Das Diagramm rechts zeigt die Anwendung der vier Gleichungen auf den Fall, bei dem statt eines porösen Materials genau eine Pore betrachtet wird. - Eine Pore? Naja, es wurde ein dünnes Metallrohr verwendet und in Kontakt mit Wasser gebracht, also die Situation der Messung der kapillaren Steighöhe dargestellt. Zur Überprüfung der Washburngleichung und der betroffenen IMETER M7 Auswertungen wurden also Testmessungen mit Einzelkapillaren durchgeführt. Da sich die Washburngleichung grundsätzlich aus dem Aufstiegsverhalten von Flüssigkeiten in Kapillaren herleitet, sollte genau dieser Fall am Modellversuch mittels einzel- Kapillar- Messungen untersucht werden. Insbesondere die Frage, ob die Washburngleichung die Infiltration in eine einzelne Kapillare beschreiben kann, obwohl hierbei die hydrostatische Kraft zwangsläufig ein sehr wichtiger Faktor wird. Wie sieht das mit der berechneten Kapillarenzahl aus? Kann die BP-Gleichung die Hydrostatik richtig berücksichtigen? (Einzelheiten vgl. Washburn/Kapillar-Flussexperiment mit einer einzelnen Kapillare (PDF)).
[So weit, so gut] Nach ausführlicher Beschäftigung mit der Thematik und der Betrachtung unterschiedlichster Probenobenarten kommen wir zum Schluss, dass die BP-Gleichung sehr gut geeignet ist, gravimetrisch beobachtbare Vorgänge mit der Mindestzahl von Anahmen erklären zu können (je weniger Variablen desto besser). Insofern sind die bereits ins Auge gefassten Effekte durch Kapillarkondensation, Dampfdruck / Kelvin-Gleichung, Advancing / Receiding - Kontaktwinkel und Kontaktwinkelgeschwindigkeit für diese Messtechnik vorerst kein Gegenstand weiterer Beschäftigung. Infiltrationsverläufe, die nicht per Washburn- oder Bosanquet-Gleichung beschrieben werden können, zeigen sich oft durch eine geeignete Parametrierung der BP-Gleichung zugänglich, wie im Folgenden noch an Beispielen gezeigt wird . Die Standardauswertung der IMETER M7-Messungen wird vorerst weiterhin mittels Washburn Gl.7 durchgeführt. Und das aus drei Gründen: sie funktioniert tatsächlich fast immer sehr gut, sie kann einfacher überprüft werden und Ergebnisse von IMETER können mit anderen Geräten/Methoden verifiziert werden und umgekehrt.
3. Test, Simulation und Korrekturen
[IMETER M7 ist ein Messgerät und ein Werkzeug] In diesem Kapitel geht es um die Möglichkeiten zu Tests und Überprüfungen betreffs und mittels IMETER Software. Insofern verlassen wir hier den werbefreien Informationsteil. IMETER M7 ist offenbar das einzige verfügbare wissenschaftliche Instrument für gravimetrische Kapillaritätsun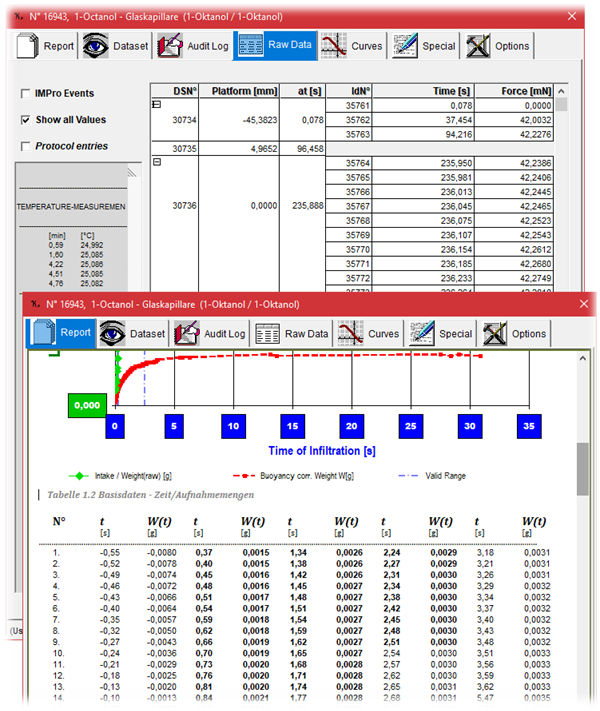 Die IMETER Software bietet transparent und einfach den Zugang zu Rohdaten und Zwischenergebnissen. Berechnungen können nachvollzogen werden; auch eigene Prüfungen und Kalkulationen können daran anschließen. Die Sachlagen können direkt kommuniziert werden.tersuchungen. Darum noch der Hinweis auf die Möglichkeiten der unabhängigen Verifikation: Grundlegendes, wie Kraftmessung, Wägung, Positionierung, Timings- und Temperaturbestimmung können unmittelbar am IMETER-System geprüft und abgesichert werden. Weitergehendes zu überprüfen, und wie all die Resultate zustande kommen, die von Schüttdichte über Kapillarradien, Oberfläche bis Oberflächenenergie und Hamaker-Konstante ein sehr weites Spektrum abdecken, wird vielfach unterstützt. Dazu dient die Ausgabemöglichkeit von Zwischenergebnissen, Berechnungsgrundlagen, Eingangsdaten und der freie, sehr unkomplizierte und unmittelbare Zugriff auf Rohdaten und die Daten erzeugende Steuerungsprogramme. Dass ein größererer Rahmen für Test, Simulation und Korrekturen gespannt wird, ist der Sache und Zielsetzung geschuldet. Die Sache, d.h. Effekte der Kapillarität, die vielgestaltig auftreten können (Pulver, Papier, Keramik, Textilien) und der Zielsetzung, dass die umfassende Bearbeitung unerhört einfach einzurichten ist. Und eigentlich ganz vor allem, dass die Anwendung so einfach sein kann, wie z.B. für ein Praktikums- oder QS Umfeld erforderlich. Um Breite abzudecken muss Breite da sein. Methodenhandhabung und Auswertung sind dafür konzipiert, von einem wenig beschränkenden Grundrahmen aus, für die Aufgabe eingehegt zu werden. Das Einhegen ist dabei aber eine Tätigkeit für Fachmänner/frauen. Diese Seite ist für solche.
Die IMETER Software bietet transparent und einfach den Zugang zu Rohdaten und Zwischenergebnissen. Berechnungen können nachvollzogen werden; auch eigene Prüfungen und Kalkulationen können daran anschließen. Die Sachlagen können direkt kommuniziert werden.tersuchungen. Darum noch der Hinweis auf die Möglichkeiten der unabhängigen Verifikation: Grundlegendes, wie Kraftmessung, Wägung, Positionierung, Timings- und Temperaturbestimmung können unmittelbar am IMETER-System geprüft und abgesichert werden. Weitergehendes zu überprüfen, und wie all die Resultate zustande kommen, die von Schüttdichte über Kapillarradien, Oberfläche bis Oberflächenenergie und Hamaker-Konstante ein sehr weites Spektrum abdecken, wird vielfach unterstützt. Dazu dient die Ausgabemöglichkeit von Zwischenergebnissen, Berechnungsgrundlagen, Eingangsdaten und der freie, sehr unkomplizierte und unmittelbare Zugriff auf Rohdaten und die Daten erzeugende Steuerungsprogramme. Dass ein größererer Rahmen für Test, Simulation und Korrekturen gespannt wird, ist der Sache und Zielsetzung geschuldet. Die Sache, d.h. Effekte der Kapillarität, die vielgestaltig auftreten können (Pulver, Papier, Keramik, Textilien) und der Zielsetzung, dass die umfassende Bearbeitung unerhört einfach einzurichten ist. Und eigentlich ganz vor allem, dass die Anwendung so einfach sein kann, wie z.B. für ein Praktikums- oder QS Umfeld erforderlich. Um Breite abzudecken muss Breite da sein. Methodenhandhabung und Auswertung sind dafür konzipiert, von einem wenig beschränkenden Grundrahmen aus, für die Aufgabe eingehegt zu werden. Das Einhegen ist dabei aber eine Tätigkeit für Fachmänner/frauen. Diese Seite ist für solche.
Die Messung an kompakten Materialien, wie Keramiken und anderen, gesinterten oder kompaktierten Stoffe ist besonders einfach, da keine weitere Präparation erforlich ist, als die Geometrie (platten- oder zylinderförmig) darzustellen und abzumessen. Um die Kohärenz mit der physikalischen Formulierung sicherzustellen, kann die Kontaktfseite zur Flüssigkeit z.B. ggf. durch eine kurze Teflonhülse geführt werden, damit ein beim Kontakt hochspringender Meniskus nicht zu seitlichen Infiltrationen führt. Ein Streifen Vaseline kann alternativ den selben Zweck erfüllen. Handhabungen dürfen fallsensitiv sein. Besonders bei weicher Materie ist nach der Infiltration die Dimension des Probekörpers nachzumessen. Hat diese sich ausgedehnt, kann der Prüfer entscheiden, ob Kapillarradien bzw. Kontaktwinkel sich auf die Ausgangs- oder Enddimensionen beziehen müssen. Ist letzteres der Fall, wird die korrigierte Geometrie angegeben. Dann bezieht sich die Auswertung auf die gequollenen oder geschwundenen Maße. Die Ergebnisse sind für solche Effekte i.d.R. sehr empfindlich. Besonders bei Messungen mit verschiedenen Fluiden zur Oberflächenenergiebestimmung findet man bei Pulvermessung diesen Effekt und muss ihn berücksichtigen. Dies kann auch dadurch erfolgen, dass die Bulkdichte des Materials in Relation zur Referenzmessung als Korrekturfaktor eingesetzt wird. Der Anwender kann grundsätzlich dazu auswählen, ob die Berechnung (1) über den Kapillarradius, (2) den Kontaktwinkel (aus Referenzmessungen, Literatur oder durch andere Bestimmungen ermittelt), (3) über einen durch die Bulkdichte korrigierten Kapillarradius oder rein über die Materialkonstante der Präparation erfolgt. Ändert man beispielsweise in einer beliebig umfänglichengroßen Messserie, den Auswertealgorithmus, so werden alle Messungen dieser Präparation automatisch entsprechend neu berechnet. So bleiben Statistikreihen und zusammengesetzte Auswertungen zur Oberflächenenergie in einer Datenbank konsistent.
[Zugriff auf Variable] Die automatische Datenauswertung der IMETER-Software verwendet die Gleichungen Gl. 6, 7, 10 und 13 innerhalb des Simulationsmoduls. Die Ergebnisse der Simulationsrechungen können mit Diagramm und Tabelle im Bericht präsentiert werden. Zu den Variablen Anfangssteighöhe h0, Startzeit t0, können durch den Prüfer die beiden Radien in r1, r2, ηL und Θ frei für Gl. 13 angegeben werden. Die Gl. 13 liefert mit r1= r2= r, ηL=0 und gleichem Θ das identische Ergebnis wie die Washburngleichung, falls die Hydrostatik keinen hinreichenden Einfluß ausübt. Man kann im Simulationsmodul auch Optimierungsfunktionen einsetzen, die die Parameter selbst findet, so dass die empirischen Steighöhen durch diese Anpassung analytisch exakt beschreibar werden. Ergänzend können die Steighöhe zu einer bestimmten Zeit oder die Zeit zu einer bestimmten Steighöhe hier interaktiv ausgerechnet werden (evtl. wurde protokolliert oder es liegen Videobilder vor).
Die verantwortlichen Variablen der Auswertung zur Kapillarkinetik sind g a, ρLuft a,c , Δρ a,b,c, γ b,c , η b,c, Θ b,c, und die geometrischen Angabenb,c (a aus der Systemeinstellung übernommen [für einzelen Messdatensätze veränderbar]; die Fallbeschleunigung g darf für Gl.13 nicht auf Null gesetzt werden; b Vorgaben über das Datenblatt der Messung veränderbar; c Angaben mit IMETER messbar und im Datenblatt einzutragen).
Test und Simulation ist eine Hilfe und wichtiger Funktionsbestandteil für wissenschaftlich denkende Prüfer und Skeptiker. Eingangsgrößen bis hin zu Komponentendaten der Oberflächenenergiebestimmung sind zugänglich ... und es wird automatisch dokumentiert! Die Richtigkeit der Stoffkonstanten kann vor oder auch nach der PUK-Messung exakt überprüft/ermittelt werden; Oberflächenspannung, Viskosität und Dichte der Messflüssigkeit können sogar in der Messzelle der PUK-Messung vor oder/und nach der Messung bestimmt werden, die Dichte des porösen Feststoffes kann zusätzlich hydrostatisch gemessen werden. Mehr kann kaum getan werden, um Prüfer in den Stand zu setzen, Messungen auf wissenschaftlichem Topniveau auszuführen.
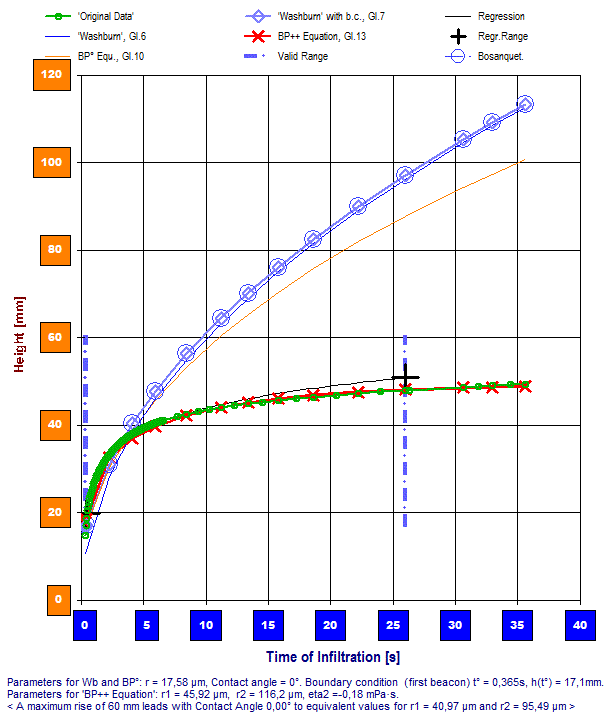
[Lösungsstrategieen] Es kommt vor, dass eine Messflüssigkeit tatsächlich nicht bis zur vollen Höhe der Probe ansteigt oder anderweitig die maximale Steighöhe bestimmt wurde. Dieser Fall ist interessant, insofern nach dem Jurin-Gesetz (Gl.10) mit der Endhöhe hfin ein Wert für r2 (·cosΘ) angebbar wird. Der Anwender kann also die Probenhöhe im Datenformular zur Messung zur tatsächlichen Steighöhe korrigieren. Die Software schlägt mit der Neuberechnung dazu automatisch passende Werte für r2 und r1 vor. Der Wert r2 stammt einfach dem Jurin-Gesetz, welches ja die finale Steighöhe bestimmt. Die Zahl für r1 folgt aus dem Verhältnis r1 = √(r2 r) [mit r = r1 ²/r2 ] und liefert die gleichen Ergebnisse, wie die Washburngleichung, allerdings unter Berücksichtigung der Schwerkraft. Zahlenwerte für r2 und r1 können vom Anwender auch frei vorgegeben werden. So können in den 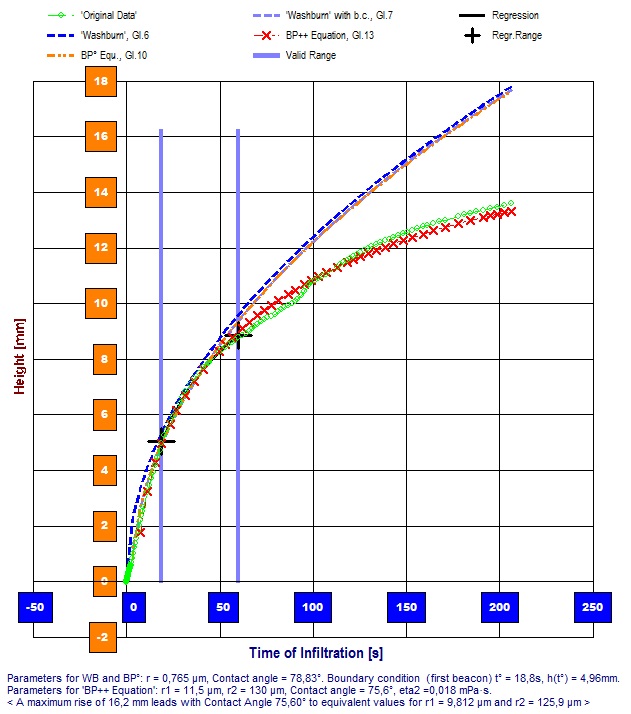 Anpassung an empirisches Verhalten durch Bestimmung analytischer Größen per Simulation und Optimierung. Zur Beschreibung der Infiltration von DMSO sind zwei Kapillarradien erforderlich. Die BP-Gleichung (Gl. 13) führt zu einem recht guten Fit! Simulationen Plots von Gl.13 mit den Messwerten verglichen und Werte für r1, r2, cosΘ und ηL, verifiziert werden. Während Washburn- und Juringleichung (Gl.6, Gl.7, Gl.10) noch einfach in Tabellenkalkulationsprogrammen berechnet werden können, ist das für die Universalgleichung (BP-Gleichung = Gl.13) kaum möglich. Zu ihr verschafft das Simulationsmodul einen bequemen Zugang. Es ist jedoch so, dass die BP-Gleichung in der Simulation nur dann sinnvoll anwendbar ist, wenn eine Zusatzinformation plausibel erschlossen werden kann oder vorliegt. Die Endsteighöhe ist dafür sehr geeignet oder evtl. Körngrößen bei Pulvern, wo man annehmen darf, dass die größte Porenweite in einer Kapillare durch diese gebildet wird.
Anpassung an empirisches Verhalten durch Bestimmung analytischer Größen per Simulation und Optimierung. Zur Beschreibung der Infiltration von DMSO sind zwei Kapillarradien erforderlich. Die BP-Gleichung (Gl. 13) führt zu einem recht guten Fit! Simulationen Plots von Gl.13 mit den Messwerten verglichen und Werte für r1, r2, cosΘ und ηL, verifiziert werden. Während Washburn- und Juringleichung (Gl.6, Gl.7, Gl.10) noch einfach in Tabellenkalkulationsprogrammen berechnet werden können, ist das für die Universalgleichung (BP-Gleichung = Gl.13) kaum möglich. Zu ihr verschafft das Simulationsmodul einen bequemen Zugang. Es ist jedoch so, dass die BP-Gleichung in der Simulation nur dann sinnvoll anwendbar ist, wenn eine Zusatzinformation plausibel erschlossen werden kann oder vorliegt. Die Endsteighöhe ist dafür sehr geeignet oder evtl. Körngrößen bei Pulvern, wo man annehmen darf, dass die größte Porenweite in einer Kapillare durch diese gebildet wird.
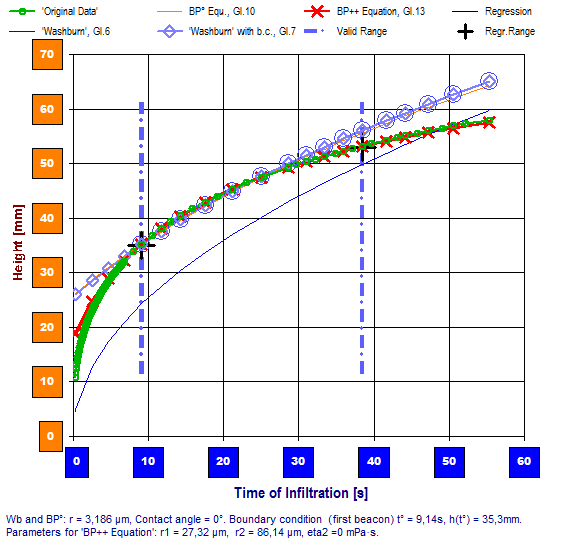
Diagramm rechts: Hier werden die beschriebenen Funktionen im IMETER-PUK Auswertemodul verwendet. Das Diagramm zeigt den auf die Steighöhe umgerechneten Verlauf der Infiltrationsmengen (grüne Kreismarken), die Graphen der Washburn-Gleichung (dunkelblau nach Gl.6), der durch hydrostatische und pneumatische Effekte ergänzten universellen Beziehung (orange Gl.10) und die Graphen der analogen, mit Anfangsbedingung berechneten Funktionswerte (hellblau Gl.7, rot Gl.13). Der Plot der BP-Gleichungen (Gl.13) schmiegt sich gut an die Steighöhenmesswerte an und fittet die Experimentaldaten sogar über den gesamten Bereich sehr gut. - Es handelt sich bei diesem Datenbeispiel um eine Messung an Maismehl bei 20°C mit Dimethylsulfoxid (DMSO) als Messflüssigkeit. - Offenbar sind die gefundenen Parameter geeignet, um diesen "Ausschnitt der Natur" zu beschreiben. - Wie konnten aber die effektiven Radien bestimmt werden, die für das Ergebnis hauptsächlich verantwortlich sind? -- Beobachtet wurde, dass die Infiltration stoppte, als die Flüssigkeitssäule 16.2 mm Höhe erreicht hat. Mit dieser Beobachtung konnte r2 zu ca. 130 µm angesetzt werden (was etwa dem Korndurchmesser bei Mehl entspricht) und per Optimierungsfunktion im Simulationsmodul wurde entsprechend r1 und der Kontaktwinkel bestimmt.
Anhand des Vergleichs der Standardabweichungen gegenüber den empirischen Daten zwischen Washburn-, BP-Gleichung und einer optimalen Regression (exponentiell, logratithmisch ...), kann das Modul direkt aufzeigen, ob eine Infiltration reglrecht erfolgt oder doch noch andere Einflüsse aufreten; beispielsweise Quellung oder atypische Sorption durch eine zu hohe Porendispersion (Schwammmaterial). Jedenfalls gibt das Simulationsmodul auch Ausgangs- und Berechnungsdaten tabellarisch aus. Dadurch können auch noch andere Theorien effektiv überprüft werden.
Die Mediumviskosität ηL (eta2) ist für Messungen an seitlich dichten Proben, wie bei Pulvern in Frittenröhrchen und rein axial permeablen Proben von 0 verschieden anwendbar. Sind hier Werte verträglich, die (bei Luftporen) größer sind als die Luftviskosität (~0,02 mPa·s) oder kommt man zu negativen Werten von ηL, (die Probenmächtigkeit übt einen Sog aus[?]), können so zumindest gewisse Effekte postuliert werden. Dass z.B. häufiger bei Flüssigkeiten mit hohem Dampfdruck (Hexan, Pentan, Ether) größere ηL-Werte zur geeigneten Anpassung erforderlich sind, kommt häufiger vor und wird einem 'Dampfdruckeffekt' zugeschrieben.
4. Porosität, Sorptivität, Oberfläche und Kapillarradien
[Innere Oberfläche]
Die Literatur gibt für den Zusammenhang zwischen spezifischer Oberfläche, Porosität und Kapillarradien eine Beziehung an [84, S.234], [12]:
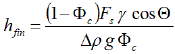 Gl. 15
Gl. 15Die Gl.15 entspricht dem Jurin-Gesetz (Gl.10), wobei der effektive Kapillarradius rc durch einen Ausdruck über die Porosität Φc und die spezifische Oberfläche FS (Gesamte Porenoberfläche pro Volumen) substituiert ist.
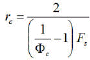 Gl. 16
Gl. 16Die Software wertet parallel eine weitere Oberflächenberechnung auf Basis der Herleitung der Washburngleichung aus. Hierfür werden die Zylinderoberflächen über den Washburn-Radius und die Kapillarenzahl bestimmt. Die Ergebnisse zeigen sich dann als brauchbar, wenn der Kontaktwinkel korrekt bestimmt oder angegeben ist.
Anders als bei der Quecksilberporosimetrie (oder BET-Oberflächenbestimmung) bezieht sich die Auswertung streng darauf, wie die Probe zur Messung vorliegt. Die Empfindlichkeit der Ergebnisse von M7 im Bezug auf den Kontaktwinkel ist äußerst stark ausgeprägt, wohingegen bei der Quecksilberporosimetrie die geringe Variabilität von Θ um 140° die Methode robust macht.
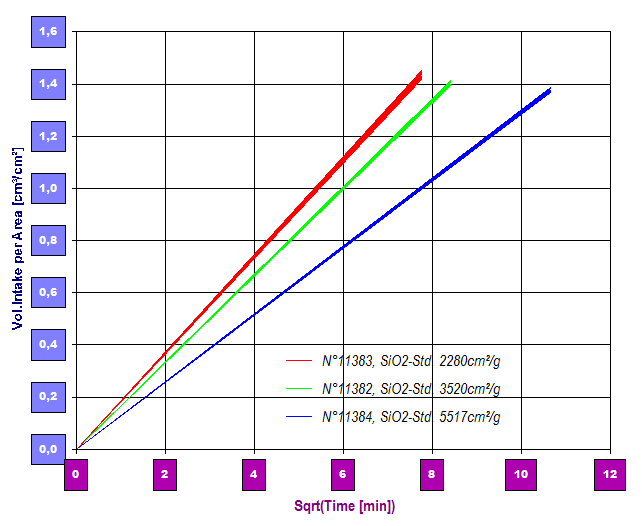 (Vergleich der Sorptivitäten: Die Steilheit der Gerade entspricht der Sorptivität, die Breite der Auffächerung gibt die jeweilige Unsicherheit an)
(Vergleich der Sorptivitäten: Die Steilheit der Gerade entspricht der Sorptivität, die Breite der Auffächerung gibt die jeweilige Unsicherheit an) Proben: SiO 2 -Oberflächenstandards durch Messungen mit Ethylenglycol (25°C, Pressdruck 90 kPa, H~30mm)
Die Messungen: für den roten Graphen 2280 cm²/g (F=6040 cm²/cm³, S=1,88 mm/√min, Φc =0,446), für grün 3520 cm²/g (F=9330 cm²/cm³, S= 1,66 mm/√min, Φc =0,457) und für blau 5517 cm²/g (F=14600 cm²/cm³, S=1,29 mm/√min, Φc =0,476). [Umrechnung nach F aus der massespezifischen Oberfläche mit der SiO 2 - Reindichte 2,65 g/cm³]. Die Kapillarradien nach Gl.16 ergeben sich als drei bis vierfach größer im Vergleich zu Resultaten der Standardauswertung (Gl.7). Sorptivität und Porosität sind linear korreliert (S = 10,61 - 19,57·Φc , r² = 0,9999), in vergleichbarer Qualität zeigen sich Sorptivität wie Porosität von der volumen-spezifischen Oberfläche abhängig (F = 33460 - 14570·S , r² = 0,9999).
Stempelgew. [Kg] IDN° ρBlk ρc Φc S rc _
0,2 11557 0,320 1,99 83,9 % 28,0 0,319
0,5 11556 0,36 2,39 84,9 % 14,8 0,200
1,0 11555 0,41 3,74 89,0 % 12,28 0,106
1,9 11554 0,47 -13,8 103 % 11,6 0,0587
3,5 11553 0,55 -6,10 109 % 8,00 0,0425
Die Tabelle gibt die Resultate dieser Testreihe wider. - Die Symbole: ρBlk Bulkdichte [g/cm³], ρc Dichte [g/cm³], Φc Porosität [%], S Sorptivität [mm/√min], rc [µm] gibt den der effektive Kapillarradius an.
Die Auswirkungen der Kompression auf Bulkdichten, Kapillarradien und Sorptivitäten sind eindeutig. DIe Saugleistung fällt, die Radien werden enger, die Dichte und die Porosität ... ?
Dichte und Porosität zeigen bei hohem Kompressionsgrad negative Werte bzw. Werte über 100%. Wie kann denn das sein? - Also, indem das Präparat mit der Infiltration expandiert, d.h. sich aufbläht, wird mehr Flüssigkeit absorbiert, als in das ursprüngliche gemessene Probenvolumen hineinpasst. Das ergibt dann irrationale Werte für ρc und Φc. Insofern: Auch wenn die IMETER-Auswertung viele Ergebnisse liefert, die eigentlich nicht gefragt sind, führt die sorgfältige und ausführliche Behandlung der zur Verfügung stehenden Informationen zu Erkenntnissen, die bisweilen Wichtigkeit entwickeln können. Beispielsweise beim 3D-Druck (mit zwei Komponenten, Pulver und Resin) kann nun gerade die so erkennbare Expansion – sie führt logischerweise durch die Aufquellung zu Präzisionsproblemen beim Drucken – gemessen und dadurch verbessert werden.
Bei der Auswertung von Messungen, kann der Anwender die Dimensionsänderung korrigieren, wenn ein Reindichte-Referenzwert zur Probe angegeben werden kann. Führt man die dort vorgeschlagene Änderung durch, dann bezieht sich die Auswertung auf die Probengeometrie nach der Infiltration.
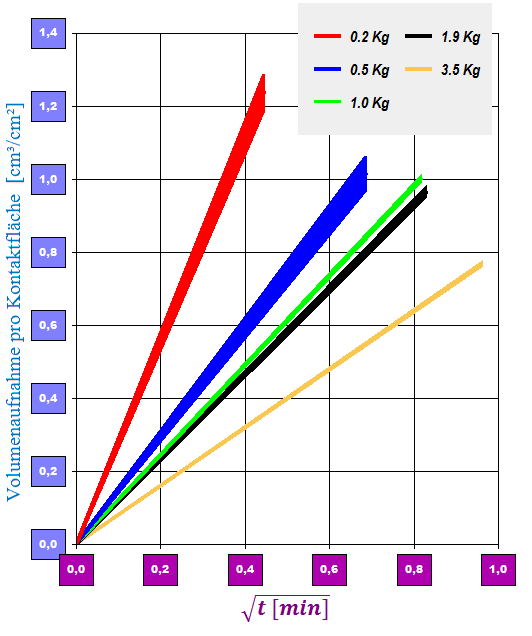 Vergleich der Sorptivität von Grafit-pulverpräparationen, die mit unterschiedlichem Druck komprimiert wurden. In diesem Diagramm, werden die ermittelten Sorptivitäten zusammen abgebildet. Je steiler der jeweilige Graph, desto höher ist die Sorptionsrate. Die keilförmige Aufspreitzung bildet die jeweilige 'Messunsicherheit' der Bestimmung ab. Die geringen Komprimierungen bei rot (0.2kg) und blau (0,5kg) führen folglich zu einer höheren 'Unsicherheit' und Sortptivität. Der höchste Pressgrad (gelb, 3.5kg) führte zu einer besseren Vorhersagbarkeit und einer starken Verringerung der Infiltrationsrate. (Prüftemperatur 20°C, Provenienz: Grafitbergbau Kaisersberg GmbH)
Vergleich der Sorptivität von Grafit-pulverpräparationen, die mit unterschiedlichem Druck komprimiert wurden. In diesem Diagramm, werden die ermittelten Sorptivitäten zusammen abgebildet. Je steiler der jeweilige Graph, desto höher ist die Sorptionsrate. Die keilförmige Aufspreitzung bildet die jeweilige 'Messunsicherheit' der Bestimmung ab. Die geringen Komprimierungen bei rot (0.2kg) und blau (0,5kg) führen folglich zu einer höheren 'Unsicherheit' und Sortptivität. Der höchste Pressgrad (gelb, 3.5kg) führte zu einer besseren Vorhersagbarkeit und einer starken Verringerung der Infiltrationsrate. (Prüftemperatur 20°C, Provenienz: Grafitbergbau Kaisersberg GmbH)[Korrektur K] Bei Kontaktwinkelmessungen ist eine korrekte Bestimmung der Kapillar- oder Materialkonstanten K die Voraussetzung. Neben den automatischen Zusammenfassungen aller Experimentaldaten, die auch Mehrfachbestimmungen von K berücksichtigt, kann der K-Wert als Mittelwert oder als Funktionsgleichung der Bulkdichte oder als Funktion der Kapillarradien zur jeweiligen Kontaktwinkelmessung berechnet werden. Das verbessert die Qualität, da so die Empfindlichkeit dieser Konstante von der Probenpräparation berücksichtigt werden kann. Die nachfolgende Tabelle zeigt ein Beispiel aus der Praxis. Es wurden drei Messungen der Kapillarkonstanten durchgeführt, wobei unterschiedliche Komprimierungen zu entsprechend verschiedenen Bulkdichten führten (je größer die Komprimierung desto größer die Bulkdichte ρBlk und desto kleiner der effektive Kapillarradius rc und die Materialkonstante K).
IDN° Fluid ρBlk rc K·cosΘ[10-17m5] Θ
11778 Hexan 0,596 0,813 28,26 0°
11820 Hexan 0,621 0,739 26,28 0°
11844 Hexan 0,652 0,534 21,02 0°
K' [m5] = ƒ(ρBlk [g/cm³]) =1,067·10-15-1,309·10-15·ρBlk mit srel.=3,1%, r²= 0,963
Mit der Tabelle wird die Funktion für den Wert von K in Abhängigkeit von der Bulkdichte ausgegeben (Standardabweichung s und Korrelationskoeffizient r² deuten eine gute Tauglichkeit an). Andernfalls könnte ganz analog über rc oder den Mittelwert der K-Wert bestimmt werden. Dieser wird ja verwendet, um in Messungen mit anderen Fluiden und mit dieser Referenz den Kontaktwinkel zu berechnen. So setzt die Auswertung in Kontaktwinkelmessungen denjenigen K-Wert ein, der zur Bulkdichte der jeweiligen Präparation gehört. K kann zusätzlich unter einem vorgegebenen Kontaktwinkel Θ bestimmt werden; eine nützliche Option, wenn beispielsweise Literatur-Daten für eine verwendete Stoffkombination vorliegen. K ist der innere Referenzwert der Präparation. Er muss nicht aus perfekten Benetzungen stammen (was gerne übersehen wird), er muss aber stimmen.
[dynamische Probenkompression] Eine Untersuchung mit einer ähnlichen Vorrichtung, bei der durch einen Stahlfederzug die Probe einem statischen Druck von ~50kPa während der Messung ausgesetzt bleibt, ergab ein bemerkenswert anderes Verhalten. Abb. rechts zeigt die Rohdaten dieser Messung. Die Infiltration wird offenbar durch den Zusatzdruck zuerst gehemmt, verläuft dann jedoch beschleunigt. Die Flüssigkeitsaufnahme erfolgt hier offenbar nicht nach einer √t-Gesetzmäßigkeit. (Probe: hochdisperser Kieselsäure (HDK 40, Wacker). Ein ähnlicher Effekt kann bei Messungen an Textilien gefunden werden. Dort führt die Zugkraft durch das Gewicht der emporsteigende Flüssigkeit zum Zusammendrängen (radiale Verdichtung) der Fasern, die dann mit kleinern Effektivradien den Lapalce-Druck erhöht. Dann kommt es darauf an, ob die Druckzunahme bei der gegebenen Viskosität über die Abbremsung der Infiltration durch engere Fließkanäle dominiert.
 *) Eine durch Probenexpansion verfälschte Dichte-Berechnung führt im Nebeneffekt zu falschen Kontaktwinkelangaben. - Daher ist die Auswertungsoption verfügbar, die die korrigierende Angabe der End-Steighöhe erlaubt (vgl. Abb.1 und Text). Weiterhin, kann in der Auswertung die Referenzdichte angegeben werden und es wird dann die relative Abweichung ausgegeben, die als weitere Kennzahl Aufschluss über das Ausmaß der Expansion oder der negativen Dilatation gibt. -- Es kommt vor, dass die Flüssigkeit nicht bis zur Probenoberfläche aufsteigt. Hier wird der hydrostatische Druck entscheidend. Die Berechung kann im Auswertungsprogramm darauf eingestellt werden. Nämlich indem die Füllhöhe nach der Messung bestimmt und in den Berechnungsoptionen angegeben wird. Mit der Korrektur werden die Experimentaldaten automatisch nochmals berechnet, wodurch die Dichtewerte den Erwartungsbereich erreichen können (sollen).
*) Eine durch Probenexpansion verfälschte Dichte-Berechnung führt im Nebeneffekt zu falschen Kontaktwinkelangaben. - Daher ist die Auswertungsoption verfügbar, die die korrigierende Angabe der End-Steighöhe erlaubt (vgl. Abb.1 und Text). Weiterhin, kann in der Auswertung die Referenzdichte angegeben werden und es wird dann die relative Abweichung ausgegeben, die als weitere Kennzahl Aufschluss über das Ausmaß der Expansion oder der negativen Dilatation gibt. -- Es kommt vor, dass die Flüssigkeit nicht bis zur Probenoberfläche aufsteigt. Hier wird der hydrostatische Druck entscheidend. Die Berechung kann im Auswertungsprogramm darauf eingestellt werden. Nämlich indem die Füllhöhe nach der Messung bestimmt und in den Berechnungsoptionen angegeben wird. Mit der Korrektur werden die Experimentaldaten automatisch nochmals berechnet, wodurch die Dichtewerte den Erwartungsbereich erreichen können (sollen). 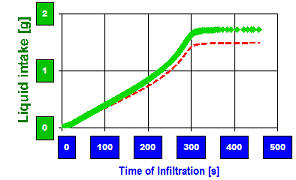
5. Materialien, Probenformen, Normal- und Sonderfälle
Die Plattformmethode PUK ist darauf eingerichtet, verschiedene Handhabungen zu Mess- und Prüfzwecken im Methodenspektrum zu begleiten. Unterhalb werden einige Beispielmessungen präsentiert, die an unterschiedlichen Materialien durchgeführt wurden, um Einsatzmöglichkeiten der IMETER-Methode N°7 "PUK" kurz für verschiedene Anwendungen vorzustellen. -- Eine Übersicht, Erklärungen zum Vorgehen und Erläuterungen der gezeigten Standarddiagrammen werden in der ► Methoden-Beschreibung gegeben.





Kompakte poröse Körper, die als Zylinder, Scheibe oder Quader vorliegen, sind sehr einfach in PUK-Messungen verwendbar.
Das Stab- oder Plattenmaterial wird in einer Halterung befestigt, angeklammert oder aufgespießt, mit dem Lastträger der Wägezelle verbunden, in der Temperier-Messzelle eingesetzt und die Messung startet ggf. nach einer Konditionierzeit. Die bei Pulverproben eingesetzten Frittenröhrchen mit erforderlichen Totmengen- und Latenzzeit-Kalibrierung fällt hier weg; und es gibt auch keine Komplikationen durch Wandeffekte der Röhrchen (...) sowie die stets empfindliche Probenpräparation.
[Mineralisch] Die Abb. rechts zeigt die Rohdaten einer archetypische Messkurve, die mit einem Stück Tafelkreide (Bild oben) erhalten wurde. Die Infiltration ist langsam, die Sorptivität entspricht etwa der von Gasbeton gegen Wasser. Der Werteverlauf folgt exakt der Washburn-Gleichung (stabförmige Probe Duchrchmesser 9,7 mm [Kreidemiene für Kreidenhalter "weiss, rund, stabfrei", Brunnen, Baier & Schneider]; Toluol als Messflüssigkeit, 25°C: S=0,6 mm/√min, r=4 nm, Φc= 25,2%).
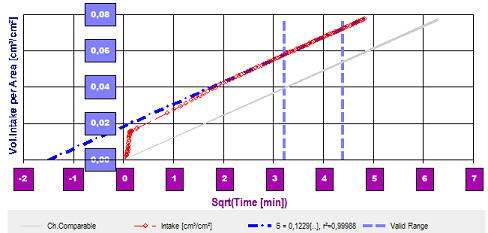 Auf die Kontaktfläche bezogene Aufnahmemenge gegen die Quadratwurzel der Zeit zeigt linear kalkulierbare Transportstöme. - Hier eine sehr geringe Sorption/Infiltration in das mikroporöse Material (Sintermetall).
Auf die Kontaktfläche bezogene Aufnahmemenge gegen die Quadratwurzel der Zeit zeigt linear kalkulierbare Transportstöme. - Hier eine sehr geringe Sorption/Infiltration in das mikroporöse Material (Sintermetall).
[Schaum- / Schwammstoff] Von einem Haushaltsschwamm (Schwammtuch, Aquapur Cleanmaster) wurde ein Streifen abgeschnitten und als Plattenmaterial gemessen, das an einem Haken aufgehängt wurde. Ohne weitere Vorbereitung wurde die Messung gegen Methanol durchgeführt. Da die Porenweite sichtbar sehr breit verteilt ist, die Infiltration die großen Poren umfließt und die Struktur eher einem invertierten Porensystem – aus "leeren Kugelpackungen" – entspricht (geschlossenporig), wurde fast schon erwartet, dass die Washburngleichung vielleicht nicht die beste Beschreibung des Fluidtransportes liefert.
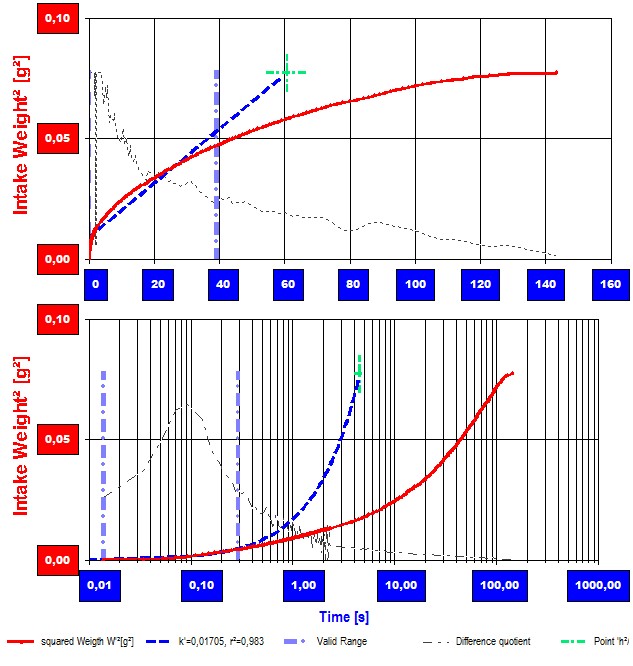
 Quadrierte Aufnahmemenge gegen die logarithmierte Zeit: Die rote Linie zeigt den hier logarithmisch sehr linearen Verlauf der Masse²-Messwerte; die blaue Kurve ist die "lineare" Infiltartionsrate. Grau gestrichelt ist der Differenzenquotient (DY/DX) eingetragen. Er gibt die Geschwindigkeitsänderung der Infiltration wider. -- Der Differenzenquotient ist normalerweise in regulären Phasen eine Konstante. Hier nicht. Solche Infiltrationsverläufe sind folglich nicht 'gesetzeskonform' .
Quadrierte Aufnahmemenge gegen die logarithmierte Zeit: Die rote Linie zeigt den hier logarithmisch sehr linearen Verlauf der Masse²-Messwerte; die blaue Kurve ist die "lineare" Infiltartionsrate. Grau gestrichelt ist der Differenzenquotient (DY/DX) eingetragen. Er gibt die Geschwindigkeitsänderung der Infiltration wider. -- Der Differenzenquotient ist normalerweise in regulären Phasen eine Konstante. Hier nicht. Solche Infiltrationsverläufe sind folglich nicht 'gesetzeskonform' .Die Abb. oben zeigt das m²/t-Diagramm mit logarithmierter Zeitachse. Das Bild dieser Infiltration ist ganz offenbar nicht typisch. Der Differenzenquozient zeigt eine anfangs beschleunigte, dann wieder abfallende Rate. Indem das als Messfluid verwendete Methanol lediglich bis zu einer Höhe von 60 mm aufstieg (Gesamthöhe des Steifens 72 mm), konnte mit r = r1²/r2 die Simulation bedient werden, um zu prüfen, ob mit zwei Kapillarradien eine Beschreibung der Infiltrationsbeschleunigung möglich ist. Tatsächlich konnte mit r1=64.5 µm und r2 =95.5 µm bei cosΘ = 0° eine grob brauchbare Beschreibung im Kontext der Washburngleichungen nach Gl.13 erreicht werden, wohingegen Washburn/Bosanquet erkennbar gar nicht passen.
Der Plot rechts führt vor, dass ein tatsächlich guter Fit (bis 50 Sekunden) erreicht werden kann (r1=45,9 µm und r2 =116.2 µm, Θ = 0° und eta2= -0.18 mPa·s).
M7 Messungen können zu sehr unterschiedlichen Zielsetzungen eingesetzt werden: Wenn im Vordergrund z.B. eine F&E-Aufgabe zur Verbesserung der Saugleistung steht, oder Input für Simulationsrechnungen zu erhalten, bietet die wortreiche Fassung des automatischen Berichs die Ausgabe einer optimalen linearen Gleichung aus einer Kleinste-Quadrate-Regression. Hier z.B. die Gleichung h(t) = 31.61+4.805·ln(t) für den Zeitbereich 3-200 Sekunden.
Die maximale Sorprivität beträgt bei 0.5 S nach Kontakt S=70 mm/√min.
 Einsatz des Simulationsmoduls, um geeignete Parameter zur formalen Beschreibung der Infiltration in das Schwammaterial zu finden: Die Grünen Markierungen zeigen die umgerechneten Messdaten. Rot ist der Verlauf der BP++-Gleichung (Gl.13) mit den entsprechenden Parameter.
Einsatz des Simulationsmoduls, um geeignete Parameter zur formalen Beschreibung der Infiltration in das Schwammaterial zu finden: Die Grünen Markierungen zeigen die umgerechneten Messdaten. Rot ist der Verlauf der BP++-Gleichung (Gl.13) mit den entsprechenden Parameter. Wenn Ihnen eine hier einkalkulierte negative Viskosität keine Probleme macht; oder möchten Sie darüber reden?
[Schwammpapier] Ein Haushaltspapier ("Wisch und Weg") verhält sich gegenüber Wasser ebenfalls nicht Washburn-typisch (Abb. unten). Ein Untersuchungsziel derartiger Materialien betrifft anwendungstypisch die Sorptivität als relevante Kennzahl. Wie im m²/t-Diagramm unten zu erkennen, fehlt ein stationärer Infiltrationsverlauf. So wird im Bereich der größten Rate zwischen 0,1 und 0,5 Sekunden die Sorptivität bei 25°C zu S=104 mm/√min bestimmt (r=41 µm, Θ = 12.5°, Φc= 55%). Um das gesamte Aufnahmevermögen – als weitere, wichtige Produkteigenschaft – in solchen Messungen zu quantifizieren, müssten kürzere Probenstücke verwendet werden.
 (m²/t-Charts: oben mit linearer unten logarithmierte X-Achse): Anders als beim zuvor präsentierten Kunstschwamm ist hier die Aufnahmerate sogar auf logarithmierter Zeitachse (unteres Diagramm) keine angenährte Gerade mehr. Die Verlaufsbeschreibung durch die Standardauswertung ist kaum sinnvoll.
(m²/t-Charts: oben mit linearer unten logarithmierte X-Achse): Anders als beim zuvor präsentierten Kunstschwamm ist hier die Aufnahmerate sogar auf logarithmierter Zeitachse (unteres Diagramm) keine angenährte Gerade mehr. Die Verlaufsbeschreibung durch die Standardauswertung ist kaum sinnvoll.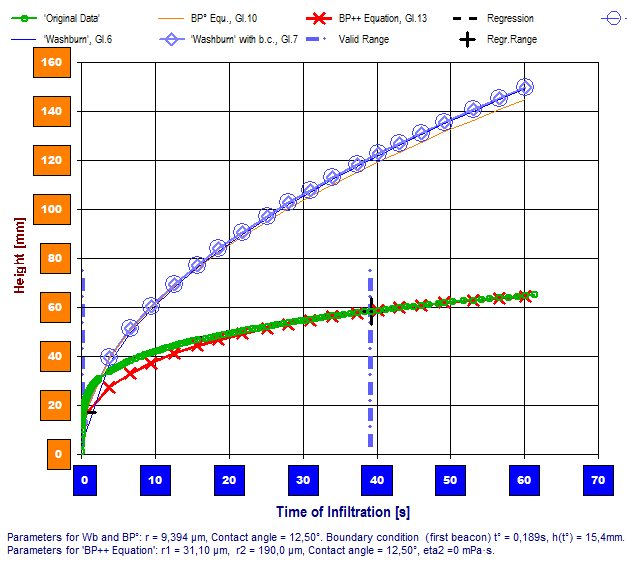 Der Graph der roten BP++- Gleichung mit den angegebenen Parameter ist zur Beschreibung des Zeitbereichs ab ca. 15 Sekunden geeignet.
Der Graph der roten BP++- Gleichung mit den angegebenen Parameter ist zur Beschreibung des Zeitbereichs ab ca. 15 Sekunden geeignet. Man kann die empirische Funktion h(t) = 25.42·t 0.2277 verwenden (diese Alternative wird von der Software vorgeschlagen) oder man teilt den zeitlichen Verlauf in Abschnitte, für die jeweils analytische Parameter bestimmt werden können.
Nach vier Sekunden hat das Lösungsmittel die Probe durch-feuchtet, danach findet eine weitere gesetzmäßige Infiltration über eine deutlich längere Dauer bei geringerer Rate statt (gegenüber Methanol verhielt sich das Holz deutlich anders). Es sieht so aus, als fände nach der ersten Infiltration in gröbere Kapillaren (Ausgewertet wurde dieser Bereich) eine Weitere in feinere Strukturen statt. (Stabförmige Probe h×d = 38,5×10,1; Toluol als Messflüssigkeit, 25°C: S=19 mm/√min, r=10 µm, Φc= 14%).
 Infiltration von Methanol in ein Textilstück (Baumwoll-Wirkgewebe).
Infiltration von Methanol in ein Textilstück (Baumwoll-Wirkgewebe). Das oberes Diagramm zeigt den Verlauf der Flüssigkeitsaufnahme; das untere die quadrierte Aufnahmemenge gegen die Zeit. Die fehl gehende blaue Gerade - d.h. der Abfall des Differenzenquotienten (grau gestrichelt) zeigt bereits, dass die Washburngleichung nicht gut geeignet sein kann, um den Verlauf analytisch zu beschreiben.
Das gleiche Ergebnis zeigte Haushaltsmaisstärke (Grafschafter). Ähnliche Verläufe zeigten sich auch zwischen Calciumphosphat und Ethylenglycol. Inwiefern aus der Löslichkeit oder einer besonderen Interaktion derartige Sorptionsverläufe hervorgehen, kann ggf. durch die Oberflächenenergieparameter (Van Oss → ΔG131) geklärt werden. Oft genug ist die Feststellung durch Messung, dass etwas passiert, ein Ergebnis.
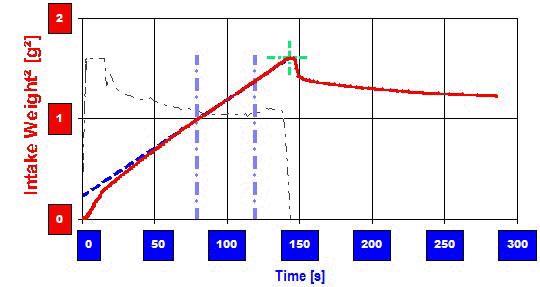 Maisstärke wird von N,N-Dimethylformamid infiltriert, es kommt zu einer bemerkenswerten Reaktion. Ab 140 s wird Masse (Lösemittel) abgegeben. Das Material verdichtet sich offenbar durch Partikelaggregation (?)
Maisstärke wird von N,N-Dimethylformamid infiltriert, es kommt zu einer bemerkenswerten Reaktion. Ab 140 s wird Masse (Lösemittel) abgegeben. Das Material verdichtet sich offenbar durch Partikelaggregation (?)6. Weiterentwicklungen
Als Mess- und Experimentalmethode ist die Beobachtung der Infiltration ein wertvolles Verfahren. Denn für die Untersuchung der materiellen Eigenschaften von Feststoffen ist mit anderen Mitteln regelmäßig eine nicht unproblematische Manipulation zur Vorbereitung der Probensubstanz notwendig. Die Präparation für eine Prüfung bzw. die Prüfung selbst verändert die Probe oder arbeitet unter Umständen, die den Rückschluß auf die in Frage stehende Eigenschaft bei der Anwendung erschweren oder gar verfälschen (z.B. für bildgebende Verfahren; Analysen mit Strahlungsquellen). Dazu kommen die selbst Unsicherheit einbringenden technischen Vorrichtungen und Sensoren (Kalibrierungen, Linearität, Querempfindlichkeiten), deren Vielheit Messaussagen verkomplizieren oder deren Messbedingungen nicht einfach kontrollierbar sind (z.B. bei mechanischen Prüfugen im Allgemeinen). Demgegenüber wird mit der IMETER Methode N°7 "PUK" schlicht das natürliche, ungezwungene Spiel von Eigenschaften über präzise, sichere Wägungen in definierter Umgebung registriert und interpretiert. Messung und Schlussfolgerungen sind verifizierbar und basieren auf unmittelbar Faktischem, was in der Festkörpermesstechnik in diesem Ausmaß eher selten der Fall ist. PUK ist ja experimentell relativ einfach, ziemlich preiswert, resourcen/energie/verbrauchs- und investitonskostenarm - leider aber in der Auswertung rechenintensiv und komplex. Und eigentlich ein hervorragendes Thema der mathematisch-physikalischen Auseinandersetzung mit der tatsächlichen Komplexität der Wirklichkeit.
[Option Test]: Das IMETER-Framework bietet durch seine Struktur und Eigenschaften Anwendungsmöglichkeiten, die Entwicklern immer erst später einfallen und Dank der formalen Behandlung dann tatsächlich recht schnell und einfach dargestellt werden können. So, wie der Volumenrestriktor (Abb.3a), der auch erst später über einem Problem eingegeben wurde, kann anderes Zubehör zur Prüfung/Entwicklung der Theorie oder zur Differenzierung von Stoffeigenschaften eingesetzt werden. Anregungen dazu:
A.  B.
B. C.
C.
[Anwendungsszenarien] Bild A. zeigt den üblichen Aufbau, nur, dass die Röhre oben gasdicht abgeschlossen ist. Die Infiltration führt zur Komprimierung der ausgetriebenen Luft und bringt sich selbst ggf. zum Stillstand. Wegen Löslichkeit von Gas in Fluid wäre eine Druckmessung, wie im Bild B., denkbar. Eine Theorieprüfung mit der Variablen "hydrostatischer Druck" ist im Bild C. angedeutet. Das Bild zeigt den Aufbau zur gravimetrischen Untersuchung der horizontal-Infiltration. Andere interessante Prüfungen könnten konische Formen zur Untersuchung von Infiltrationsvorgängen verwenden (sich verjüngende oder trichterförmig erweiternde Kegel) oder den Einbau von Eng- oder Erweiterungsstellen vorsehen.
[Steighöhe - visuell] Geräte mit Schnittstelle können allgmein in die IMETER-Steuerung (auch vom Benutzer) aufgenommen werden. EIne extra Webcam wurde zwischenzeitlich auch einmal anprogrammiert (Das geht schon. Aber wir brauchen es angesichts des Aufwands, bis so etwas richtig funktioniert, eigentlich nicht). In einigen Fällen wäre es gleichwohl schon hilfreich gewesen, wenn zeitsynchrone Bilder verfügbar gewesen wären ...
[Porosität, Dichte] Um Porosität und Dichte der Probe nach der Infiltration zu prüfen bzw. die stets automatisch von der Software erfolgte Berechnung der selben zu verifizieren, könnte mit entsprechend dimensioniertem Messgefäß und Probe nach der Infiltration eine vollständige Versenkung in der Messflüssigkeit durchgeführt werden, um so das Gesamtvolumen zu bestimmen (... natürlich immer alles als Option und zur automatischen Durchführung).
[konkurrierende Benetzung] Weiterhin wurde noch nicht geprüft, wie die PUK-Messung mit zwei nicht mischbaren flüssigen Phasen verläuft. Wobei also anstelle von Luft ein von der Probe durchtränktes, anders liquides Medium tritt. Der Kontaktwinkel ist in diesem Fall der, der sich in der Dreiphasengrenze beider Flüssigkeiten mit dem Feststoff bildet.
[Perkolationsexperiment] Die Pulverprobe in einem Röhrchen oder aus einem (z.B.) zylindrischen Stabmaterial (Pressling, Sinterteil oder Kompaktat) kann an der Wägezelle aufgehängt werden und mit lichtem Spalt über einem passenden, saugfähigen Untergrund stehen. Wie bei einer Chromatographiesäule wird oben Flüssigkeit entsprechend aufgebracht und die Dosierung so geregelt, dass die Probe nicht überläuft. Irgendwann ist die Probe durchfeuchtet und gibt unten die überschüssige Flüsigkeit nach unten ab. Die Pumpgeschwindigkeit wird so geregelt, dass ein stationäres Gewicht gemessen wird. Das Gewicht der im Gleichgewicht befindlichen Flüssigkeitsmenge gibt über das zugängliche Porenvolumen Auskunft. Und auf die Durchsickergeschwindigkeit kann die Hagen-Poseuille-Gleichung entsprechend angesetzt werden. So kann eine weitere Klärung und Prüfung der Grundlagen erfolgen oder eine weitere Materialeigeschaft geprüft werden. Oder soll r1 für die BP-Gleichung (Gl.13) per Durchflussmessung bestimmt werden? Der Volumenstrom bei Aufgabe von Flüssigkeit auf ein gefülltes Röhrchen kann also auch dafür bestimmt werden. -- Solche Experimente zu regeln, ist für die IMETER Steuerung jedenfalls kein Problem.
[Infiltrationszeitspektrum, Kapillarradien] Mit der Variation der Probenlänge kann eine differenziertere Kapillarkinetik aufgestellt werden. Indem der Sorptionsgeschwindigkeitseffekt des Probenendes bei verschiedenen Probenlängen konstant bliebt, kann die relative Steilheit des Abfallens der Infiltrationsgeschwindigkeit beim Erreichen des Probenendes für die verzögerte und verdeckte Infiltrationskinetik gedeutet werden. Vielleicht kann darauf ein Verfahren für die Bestimmung der mittleren Maximal- und Minimal- kapillarradien aussehen.
[Entwicklung]: Die Methode liefert auf Probeneigenschaften und Handhabungen gute Rückkopplungen in Form der mehrere Qualitäten umfassenden Ergebnisse. Die überexperimentelle und automatische Auswertung von Messserien, die durch das IMETER-Framework geleistet wird und Experimentaldaten zur Bestimmung der Oberflächenenergie zusammenfasst und organisiert, zeigte Widersprüche, wenn die eine oder andere Flüssigkeit besondere Wechselwirkungen mit der Probe aufwies: Sind die Komponentendaten nicht korrekt? Jedenfalls musste darum eine lautere Möglichkeit zum Ausblenden von Datensätzen in der Auswertungssoftware eingebaut werden. Weil auch noch unterschiedliche Oberflächenenergie-Komponentendaten und Theorien kursieren, musste die Möglichkeit zur Kalkulation nach verschiedenen Algorithmen und mit verschiedenen Konstanten in der Auswertungssoftware eingebaut werden. Da Komponentendaten evtl. nicht korrekt sein können, werden auch deren Einflüsse (OGC-Tabellen) auseinandergesetzt.
Im Simulationsmodul wurde die Bosanquet-Gleichung [14] zur vergleichenden Auswertung gegenüber Washburn- und BP-Gleichung eingesetzt. Wahrscheinlich wird sie aber wieder aus der Auswertung verschwinden, da durch Ihren Gebrauch bisher absolut kein Nutzen zu erkennen ist. Falls der Nutzerkreis zustimmt, soll zur nächsten Überarbeitung statt Bosanquet die Formulierung aus [9] versucht werden.
Sofern bessere Modelle verfügbar werden, sind auch bereits durchgeführte Messungen nicht vergeblich ausgeführt worden. Denn: das IMETER-Framework speichert immer geordnete Rohdaten und erlaubt zu jeder Zeit deren Neuberechung - dann evtl. mit optimierter Theorie, sprich besserer Brille.
[Weiterentwicklungen]: Wir prüfen vorliegende und hinzukommende Messdaten gerne durch neue Theorien. Unsere Anstrengungen in diese Richtung – um gewisse Schwierigkeiten, die sich aus Testreihen ergaben, aufzuklären – betrafen die Einbeziehung von Dampfdruckdaten (Kelvin-Gleichung), um so über diese mutmaßlich wichtige Druckkomponente und im Zusammenhang mit dem Spreitungsdruck vielleicht eine bessere Korrelationen zu erreichen. Wir würden es begrüßen, wenn sich ambitionierte Forscher, die Versuchsdesigns / mathematische Formulierungen evtl. unter Betrachtung in Frage stehenden Einflüsse (Polarisierbarkeit / Dipolmoment, Kohäsionsenergie-dichte, osmotischen Effekte, Θadv/rec ...) begleiten wollten. Besonders von praktischer Relevanz wäre es, wenn statt reinen Flüssigkeit auch Mischungen [Wasser/NaCl, Wasser/Isopropanol ...] zur Oberflächenenergiemessung und Berechung eingesetzt werden könnten. Wie kann aus dem Abklingen der Sorptionsgeschwindigkeit bei Erreichen der Oberfläche die Kapillardispersion bestimmt werden? Es steht auch noch die Formulierungen über mixed-mode Kapillarfluß/Ringspaltfluß sowie Infiltartionsrichtung relativ zum Schwerkraftvektor zur praktischen Prüfung an. Jedenfalls, nebst der Messunsicherheit / Fehlerfortpflanzung (vor der einem nur grauen kann) gibt es da also noch einiges für M7 im "IMETER Work-in-Progress-Projekt" ;-)
Ausprobieren?
Nutzen Sie doch einfach unsere Dienste für Messungen von Sorptivität bis Kontaktwinkel/Oberflächenenergie - wir stehen zu Ihrer Verfügung!
8. Literatur, Links, Hinweise:
[1] bei Wolfgang Ostwald in der nicht-Laplace/Poiseuille- Form (explizit "h(t)= f·tm") aber mit umfangreichen Daten: "Über das Zeitgesetz des kapillaren Aufstiegs von Flüssigkeiten und über die Beziehungen desselben zur chemischen Konstitution der letzteren", Colloid & Polymer Science, Vol. 2 (1908), S.20-49.
[2] Bell, J.M. and Cameron, F.K., "The flow of liquids through capillary spaces". J. Phys. Chem. 10 (1906), S.658–674.
[3] R. Lucas, Über das Zeitgesetz des kapillaren Aufstiegs von Flüssigkeiten. Kolloid. Z. 23 (1918), S.15.
[4] E. W. Washburn, Phys. Rev. 273 (1921), S.17.
[5] Dissertation von Sabrina Gericke, Oberflächenmodifizierung von Lactose mit überkritischem CO2, Bonn 2003, http://nbn-resolving.de/urn:nbn:de:hbz:5n-02589, S.21ff (Dortige Quellenbezeichnung: Yurtseven, N., Stabilitätsuntersuchung an festen Arzneiformen am Beispiel der Acetylsalicylsäure, Dissertation Bonn 1997.)
Zahlreiche Fundstellen in Lehr- und Textbüchern zum Thema: [83, S.324; 84, S.130; 79, S.335 (mit Quecksilberporosimetrie); 71, S.139 (mit Dünnschicht-Technik); 67, S.470 (mit zwei Fluiden)].
[6] Referiert zahlreiche Fundstellen, Methodenwürdigung, Anwenndungen: Trong Dang-Vu, Jan Hupka, Characterization of porous materials by capillary rise method, Physicochemical Problems of Mineral Processing, 39 (2005), 47-65.
[7] Neirinck, van Deursen, Van der Biest, Vleugelsw, Wettability Assessment of Submicrometer Alumina Powder Using a Modified Washburn Method, J. Am. Ceram. Soc., 93 [9] 2515-2518 (2010), DOI: 10.1111/j.1551-2916.2010.03854.x.
[8] Dimitrov, Milchev, Binder, Forced Imbibition - a Tool for Determining Laplace Pressure, Drag Force and Slip Length in Capillary Filling Experiments, DOI: 10.1039/b719248g Cite as: arXiv:0712.2331v1 [physics.flu-dyn].
[9] H.T. Xue, Z.N. Fang, Y. Yang, J.P. Huang, L.W. Zhou, Contact angle determined by spontaneous dynamic capillary rises with hydrostatic effects: Experiment and theory, Chemical Physics Letters 432 (2006) 326–330.
[10] Debdutt Patro, Saswata Bhattacharyya, Vikram Jayaram, Flow Kinetics in Porous Ceramics: Understanding with Non-Uniform Capillary Models, J. Am. Ceram. Soc., 90 [10] 3040–3046 (2007) DOI: 10.1111/j.1551-2916.2007.01776.x.
[12] Marmur, A., Penetration and Displacement in Capillarysystems, Modern Approaches to Wettability, Schrader, M. E. and Loeb, G. I. (Eds), Plenum Press, New York, 1992 (Referiert in: Grundke, K.,: Wetting, Spreading and Penetration, in: Handbook of Applied Surface and Colloid Chemistry, Krister Holmberg, Ed., Vol.2, John Wiley & Sons Ltd, 2002).
[13] Tiberg, F., Daicic, J., Froberg, J., Surface Chemistry of Paper, in: Handbook of Applied Surface and Colloid Chemistry, Krister Holmberg, Ed., Vol.1, John Wiley & Sons Ltd, 2002, S.160.
[14] Loeb, G.I., Schrader, M.E. (Hg.), Modern Approaches to Wettability: Theory and Applications, Springer Science & Business Media, 2013.
[15] Nicolas Fries, Capillary transport processes in porous materials – experiment and model; Cuvillier Verlag Göttingen; 2010; ISBN 978-3-86955-507-2, book is available at www.cuvillier.de (https://www.flow3d.com/wp-content/uploads/2014/08/Capillary-transport-processes-in-porous-materials-%E2%80%93-experiment-and-model.pdf). Leider wurde diese sehr interessante Arbeit erst nach der 2. Überarbeitung von M7 gefunden.